|
Единый государственный экзамен по математике, 2004 год
Скачать pdf-файл.
Часть A
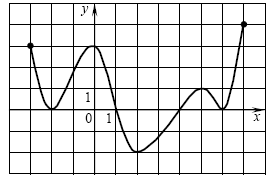 A1. Функция задана графиком. Укажите промежуток, на
котором она принимает только отрицательные значения. A1. Функция задана графиком. Укажите промежуток, на
котором она принимает только отрицательные значения.
Решение. Функция отрицательна на тех промежутках, на которых ее
график лежит ниже оси абсцисс; для заданной функции это интервал
(1; 4).
Правильный ответ: 2.
A2. Найдите множество значений функции 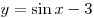 . .
Решение. В силу ограниченности функции 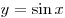 и свойств неравенств имеем:
и свойств неравенств имеем:
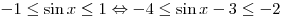 . .
Правильный ответ: 4.
A3. Найдите производную функции 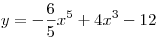 . .
Решение. Поскольку 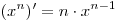 и и 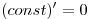 , пользуясь правилами дифференцирования, получаем: , пользуясь правилами дифференцирования, получаем:
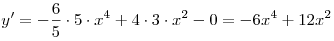 . .
Правильный ответ: 2.
A4. Укажите область определения функции 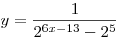 . .
Решение. Область определения функции задается неравенством 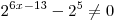 . Имеем: . Имеем:
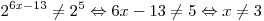 . .
Правильный ответ: 3.
A5. Вычислите 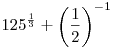 . .
Решение. Поскольку 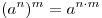 , имеем: , имеем:
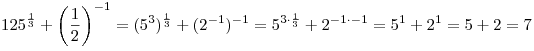 . .
Правильный ответ: 1.
A6. Упростите выражение ![\frac{\sqrt[5]{a^{11}}}{\sqrt[5]{a}} \frac{\sqrt[5]{a^{11}}}{\sqrt[5]{a}}](/inc/pictures/d7847b2d1ccd1a69629ccb30ca906448.png) . .
Решение. Поскольку ![\sqrt[n]{a^m} = a^{\frac{m}{n}} \sqrt[n]{a^m} = a^{\frac{m}{n}}](/inc/pictures/cdd70cbc67c0c3af89bbc72fa204239d.png) и и 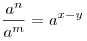 , получаем: , получаем:
![\frac{\sqrt[5]{a^{11}}}{\sqrt[5]{a}} = a^{\frac{11}{5}} : a^{\frac{1}{5}} = a^{\frac{11}{5} - \frac{1}{5}} = a^{\frac{10}{5}} = a^2 \frac{\sqrt[5]{a^{11}}}{\sqrt[5]{a}} = a^{\frac{11}{5}} : a^{\frac{1}{5}} = a^{\frac{11}{5} - \frac{1}{5}} = a^{\frac{10}{5}} = a^2](/inc/pictures/14d365f39b5fdb5a578af90b0f131eac.png) . .
Правильный ответ: 3.
A7. Вычислите 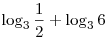 . .
Решение. Используя формулу преобразования суммы логарифмов в
логарифм произведения, имеем:
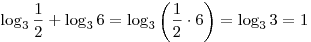 . .
Правильный ответ: 1.
A8. Решите неравенство 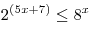 . .
Решение. Перейдем к основанию степени 2 и воспользуемся
возрастанием показательной функции, с основанием большим единицы:
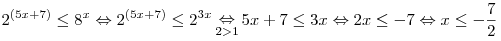 . .
Правильный ответ: 4.
A9. Какому промежутку принадлежит корень уравнения 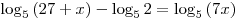 ? ?
Решение. Пользуясь теоремами равносильности, последовательно
получаем:
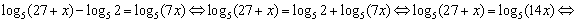
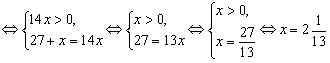 . .
Найденный корень принадлежит промежутку (2; 4).
Правильный ответ: 2.
A10. Решите неравенство 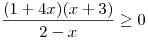 . .
Решение. Решим данное неравенство методом интервалов (см.
рис.):
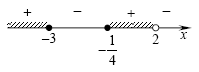
Правильный ответ: 2.
A11. Решите уравнение 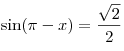 . .
Решение. Последовательно получаем:
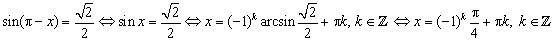 . .
Правильный ответ: 3.
A12. К графику функции 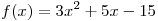 в точке с абсциссой в точке с абсциссой 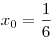 проведена касательная. Найдите тангенс угла наклона касательной к оси
Ox.
проведена касательная. Найдите тангенс угла наклона касательной к оси
Ox.
Решение. Тангенс угла наклона к оси Ox касательной к
графику функции, проведенной в его точке с абсциссой
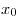 , равен значению производной данной функции в точке , равен значению производной данной функции в точке
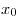 . Найдем производную и вычислим ее значение в
заданной точке: . Найдем производную и вычислим ее значение в
заданной точке:
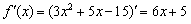 . .
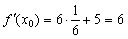 . .
Правильный ответ: 1.
A13. Найдите значение 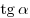 , если , если 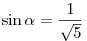 и и 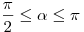 . .
|
1.
|
–2
| |
2.
|
2
| |
3.
|
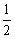
| |
4.
|
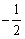
|
Решение. Поскольку число 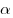 лежит во второй координатной четверти, его косинус отрицателен, откуда лежит во второй координатной четверти, его косинус отрицателен, откуда
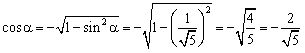 . .
Тогда
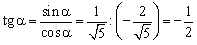 . .
Правильный ответ: 4.
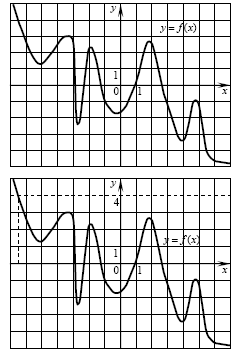 A14. На рисунке изображен график функции A14. На рисунке изображен график функции  . Какому из следующих промежутков принадлежит корень уравнения . Какому из следующих промежутков принадлежит корень уравнения 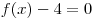 ? ?
Решение. Уравнение 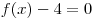 равносильно уравнению
равносильно уравнению 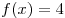 . Найдем точку графика с ординатой равной 4, и определим ее абсциссу
(см. рис.). Найденное число лежит в промежутке . Найдем точку графика с ординатой равной 4, и определим ее абсциссу
(см. рис.). Найденное число лежит в промежутке 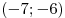 . .
Правильный ответ: 3.
Часть B
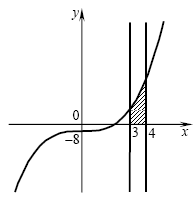 B1. Вычислите площадь фигуры, ограниченной линиями B1. Вычислите площадь фигуры, ограниченной линиями 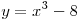 , , 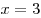 , , 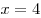 , , 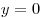 . .
Решение. Изобразим на рисунке эскизы графиков функций 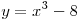 , , 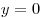 , и прямые , и прямые 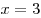 , , 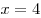 . Фигура, площадь которой требуется найти, на рисунке заштрихована.
Площадь этой фигуры S дается формулой . Фигура, площадь которой требуется найти, на рисунке заштрихована.
Площадь этой фигуры S дается формулой 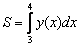 : :
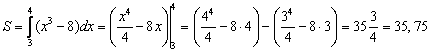 . .
Правильный ответ: 35,75.
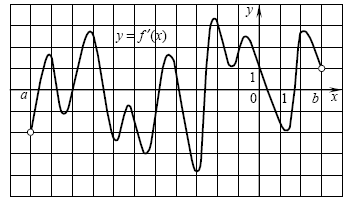 B2. Функция B2. Функция  определена на промежутке определена на промежутке 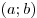 . На рисунке изображен график ее производной. Укажите число точек
максимума функции . На рисунке изображен график ее производной. Укажите число точек
максимума функции  на промежутке на промежутке 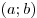 . .
Решение. Дифференцируемая
функция достигает максимума в некоторой точке, если в левой
полуокрестности этой точки ее производная положительна, а в
правой — отрицательна. На заданном графике таких точек
четыре.
Правильный ответ: 4.
B3. Найдите значение выражения 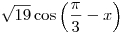 , если , если 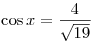 и и 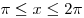 . .
Решение. Поскольку 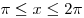 , имеем: , имеем:
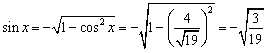 . .
Далее, используя формулу 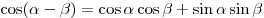 , получаем: , получаем:
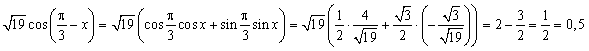 . .
Правильный ответ: 0,5.
B4. Сколько корней имеет уравнение 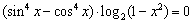 ? ?
Решение. Поскольку 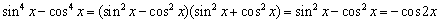 , получаем: , получаем:
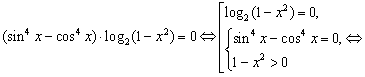
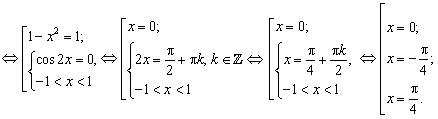
Таким образом, данное уравнение имеет три корня.
Правильный ответ: 3.
B5. Найдите точку минимума функции 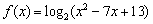 . .
Решение. Поскольку логарифмическая функция с основанием большим
единицы монотонно возрастает, точка минимума заданной функции совпадает
с точкой минимума квадратного трехчлена 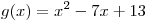 , если он положителен в этой точке. Квадратный трехчлен , если он положителен в этой точке. Квадратный трехчлен 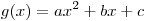 с положительным старшим коэффициентом достигает минимума в точке
с положительным старшим коэффициентом достигает минимума в точке 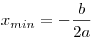 . В нашем случае: . В нашем случае: 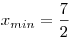 , тогда , тогда
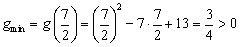 . .
Таким образом, число 3,5 — искомая точка минимума функции 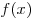 . .
Правильный ответ: 3,5.
B6. Укажите наибольшее целое число из области определения
функции 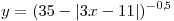 . .
Решение. Область определения данной функции задается
неравенством 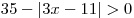 . Решим его: . Решим его:
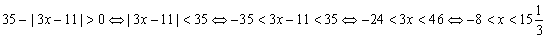 . .
Тем самым область определения данной функции есть интервал 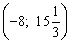 . Наибольшее целое число из этого интервала равно 15. . Наибольшее целое число из этого интервала равно 15.
Правильный ответ: 15.
B7. На каждый из нескольких опытных участков внесли два
удобрения. Первое вносили по такой схеме: 0,5 кг — на первый
участок, а на каждый следующий участок на 0,5 кг больше, чем на
предыдущий. Второе удобрение вносили по 3 кг на каждый участок.
Всего внесли 42 кг удобрений. На сколько участков внесли
удобрения?
Решение. Пусть искомое число участков n. Используя
формулу суммы первых n членов арифметической прогрессии 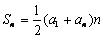 , получим количество внесенных килограммов первого удобрения: , получим количество внесенных килограммов первого удобрения:
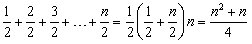 . .
Поскольку второго удобрения внесли 3n кг, а всего внесли 42 кг
удобрений имеем уравнение: 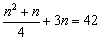 , откуда: , откуда:
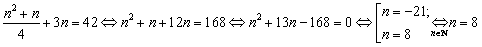 . .
Таким образом, удобрения внесли на 8 участков.
Правильный ответ: 8.
B8. В правильной треугольной пирамиде SABC сторона
основания равна 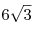 , а боковое ребро наклонено к плоскости основания ABC под
углом, тангенс которого равен , а боковое ребро наклонено к плоскости основания ABC под
углом, тангенс которого равен 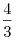 . Найдите площадь треугольника MSC, где M —
середина отрезка AB. . Найдите площадь треугольника MSC, где M —
середина отрезка AB.
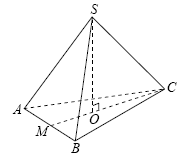 Решение. Пусть SO — высота пирамиды
(см. рис.). Поскольку пирамида правильная, ее основанием является
равносторонний треугольник, а точка О — его центр, Решение. Пусть SO — высота пирамиды
(см. рис.). Поскольку пирамида правильная, ее основанием является
равносторонний треугольник, а точка О — его центр, 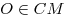 . .
Отрезок CM — медиана, и, следовательно, высота
правильного треугольника ABC, откуда 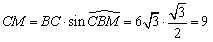 . .
Отрезок СO – радиус окружности, описанной около
треугольника ABC, следовательно, 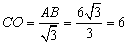 . .
Поскольку угол между боковым ребром и плоскостью основания есть угол
между наклонной SC
и ее проекцией на плоскость основания CO, имеем 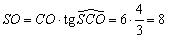 . .
Окончательно имеем: 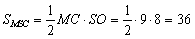 . .
Правильный ответ: 36.
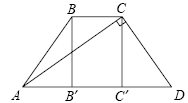 B9. В равнобедренной трапеции основания равны 9 и 15,
диагональ перпендикулярна боковой стороне. Найдите площадь трапеции. B9. В равнобедренной трапеции основания равны 9 и 15,
диагональ перпендикулярна боковой стороне. Найдите площадь трапеции.
Решение. Пусть ABCD — заданная трапеция, 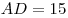 , , 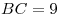 , , 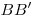 и и 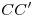 — высоты трапеции (см. рис.). — высоты трапеции (см. рис.).
Заданная трапеция равнобедренная, поэтому:
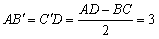 , ,
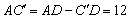 . .
Отрезок 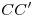 – высота прямоугольного треугольника ACD, опущенная из
вершины прямого угла С на гипотенузу AD, откуда
– высота прямоугольного треугольника ACD, опущенная из
вершины прямого угла С на гипотенузу AD, откуда
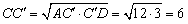 . .
Тогда
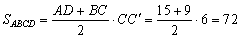 . .
Правильный ответ: 72.
Часть C
C1. Решите систему уравнений 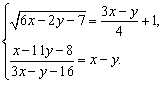
Решение. Рассмотрим первое уравнение системы. Пусть 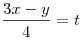 , тогда , тогда 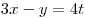 , , 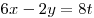 и уравнение принимает вид и уравнение принимает вид 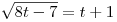 . Имеем: . Имеем:
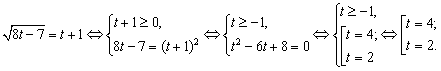
Таким образом, возможны два случая: 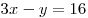 или или 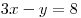 . .
Если 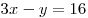 система не имеет решений, так как знаменатель левой части второго
уравнения обращается в нуль.
система не имеет решений, так как знаменатель левой части второго
уравнения обращается в нуль.
Рассмотрим случай 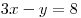 . Имеем: . Имеем:
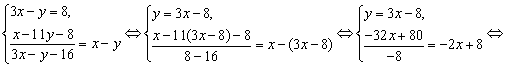
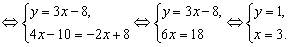
Таким образом, исходная система
уравнений имеет одно решение: 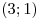 . .
Ответ: 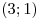 . .
C2. Найдите наименьшее значение периметра прямоугольника
со сторонами, параллельными осям координат, и с диагональю OM,
где O — начало координат, а M — точка на
графике функции 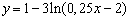 , , 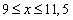 . .
Решение. Пусть абсцисса точки М равна х, тогда ее
ордината y равна 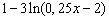 . .
Заметим, что функция 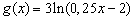 возрастает на своей области определения — открытом луче
возрастает на своей области определения — открытом луче 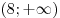 , и обращается в нуль в точке 12. Поэтому заданная функция , и обращается в нуль в точке 12. Поэтому заданная функция 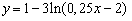 убывает промежутке
убывает промежутке 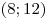 и принимает на только положительные значения. Это означает, что для
всех х из отрезка
и принимает на только положительные значения. Это означает, что для
всех х из отрезка ![[9; 11,\!5] [9; 11,\!5]](/inc/pictures/4894ebb336c67659af9a195808630b3b.png) точка
точка 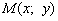 лежит в первой четверти.
лежит в первой четверти.
Тогда, периметр прямоугольника равен 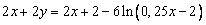 . Осталось найти наименьшее значение функции . Осталось найти наименьшее значение функции 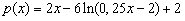 на отрезке
на отрезке ![[9; 11,\!5] [9; 11,\!5]](/inc/pictures/4894ebb336c67659af9a195808630b3b.png) . .
Найдем производную функции 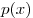 : :
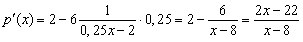 . .
Найденная производная обращается в нуль в точке 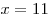 , отрицательна на полуинтервале , отрицательна на полуинтервале 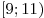 и положительна на полуинтервале
и положительна на полуинтервале ![(11; 11,\!5] (11; 11,\!5]](/inc/pictures/762bdc05a9ade9152b28922930daf29c.png) . Тем самым точка . Тем самым точка 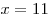 — точка минимума, причем это единственная точка экстремума непрерывной на заданном отрезке функции. Поэтому — точка минимума, причем это единственная точка экстремума непрерывной на заданном отрезке функции. Поэтому 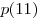 есть наименьшее на отрезке
есть наименьшее на отрезке ![[9; 11,\!5] [9; 11,\!5]](/inc/pictures/4894ebb336c67659af9a195808630b3b.png) значение исследуемой функции. Найдем его:
значение исследуемой функции. Найдем его:
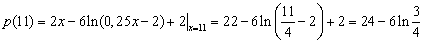 . .
Таким образом, наименьшее значение периметра прямоугольника равно 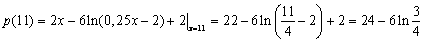 . .
Ответ: 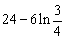 . .
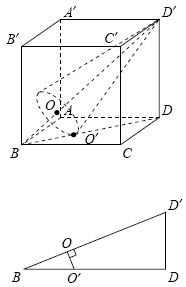 C3. В кубе C3. В кубе 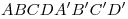 с ребром, равным
с ребром, равным 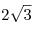 , расположен конус. Вершина конуса находится в точке , расположен конус. Вершина конуса находится в точке 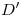 , а центр его основания, точка O, лежит на диагонали , а центр его основания, точка O, лежит на диагонали 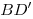 так, что так, что 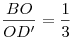 . Окружность основания конуса имеет с каждой гранью, содержащей точку B, ровно по одной общей точке. Определите объем конуса. . Окружность основания конуса имеет с каждой гранью, содержащей точку B, ровно по одной общей точке. Определите объем конуса.
Решение. Длина диагонали основания куба равна 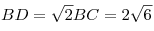 ; длина диагонали куба равна ; длина диагонали куба равна 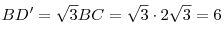 , тогда , тогда 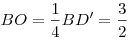 , , 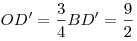 — это длина высоты конуса. — это длина высоты конуса.
Пусть точка 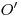 – точка касания основания конуса с основанием
ABCD данного куба. Рассмотрим сечение куба и конуса плоскостью – точка касания основания конуса с основанием
ABCD данного куба. Рассмотрим сечение куба и конуса плоскостью
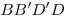 . Эта плоскость является плоскостью симметрии как квадрата
ABCD, так и окружности основания конуса. Окружность основания
конуса имеет с гранью ABCD ровно одну общую точку,
следовательно, эта точка принадлежит плоскости симметрии, откуда
следует, что точка . Эта плоскость является плоскостью симметрии как квадрата
ABCD, так и окружности основания конуса. Окружность основания
конуса имеет с гранью ABCD ровно одну общую точку,
следовательно, эта точка принадлежит плоскости симметрии, откуда
следует, что точка 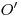 лежит на диагонали основания BD. лежит на диагонали основания BD.
Поскольку прямоугольные треугольники 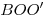 и и 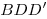 имеют общий угол В, они подобны, что позволяет найти радиус основания конуса — отрезок имеют общий угол В, они подобны, что позволяет найти радиус основания конуса — отрезок 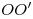 (см. рис.): (см. рис.):
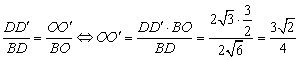 . .
Тогда
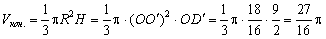 . .
Ответ: 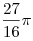 . .
C4. Найдите все положительные значения параметра a,
при каждом из которых множество решений неравенства 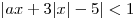 содержится в некотором отрезке длиной 20 и при этом содержит
какой-нибудь отрезок длиной 10.
содержится в некотором отрезке длиной 20 и при этом содержит
какой-нибудь отрезок длиной 10.
Решение. Решим данное неравенство при 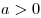 : :
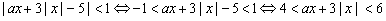 . .
Если 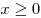 , имеем , имеем
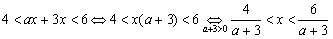 , ,
причем, все числа из интервала 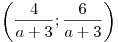 удовлетворяют условию удовлетворяют условию 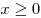 . .
Если 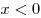 , имеем , имеем
.
В зависимости от знака выражения  , рассмотрим два случая: , рассмотрим два случая:
а) если 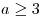 , то неравенство , то неравенство 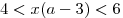 , а вместе с ним и исходное неравенство не
имеют отрицательных решений; , а вместе с ним и исходное неравенство не
имеют отрицательных решений;
б) если 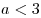 , имеем , имеем
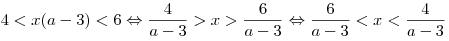 , ,
причем все числа из интервала 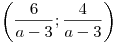 , удовлетворяют условию , удовлетворяют условию 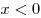 . .
Таким образом, при 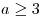 множество решений заданного неравенства есть интервал
множество решений заданного неравенства есть интервал 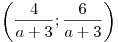 , а при , а при 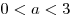 — объединение интервалов:
— объединение интервалов: 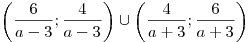 . .
Осталось определить, при каких значениях параметра множество решений
содержится в некотором отрезке длиной 20 и при этом содержит
какой-нибудь отрезок длиной 10.
Поскольку 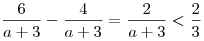 при
при 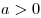 , интервал , интервал 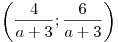 не содержит ни одного отрезка длиной 10. Следовательно, значения не содержит ни одного отрезка длиной 10. Следовательно, значения 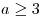 не удовлетворяют условию задачи. не удовлетворяют условию задачи.
Множество 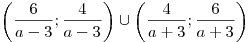 содержится в некотором отрезке длиной 20 и при этом содержит
какой-нибудь отрезок длиной 10, тогда и только тогда, когда
одновременно выполняются два условия
содержится в некотором отрезке длиной 20 и при этом содержит
какой-нибудь отрезок длиной 10, тогда и только тогда, когда
одновременно выполняются два условия 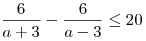 и и 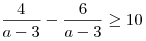 . Решим соответствующую систему для . Решим соответствующую систему для 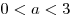 : :
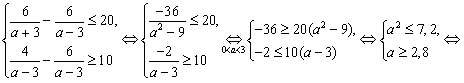
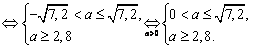
Полученная система не имеет решений, поскольку 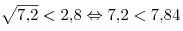 . Это означает, что множество решений неравенства . Это означает, что множество решений неравенства 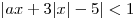 не может одновременно содержаться в отрезке длины 20 и содержать
отрезок длины 10. не может одновременно содержаться в отрезке длины 20 и содержать
отрезок длины 10.
Ответ: таких значений параметра а не существует.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
