Механика и гидростатика. Ответы
- Палка будет плавать на глубине 20 м.
- Вода втрубке находится на высоте 0,53 см.
- Высота подъема поршня равна 6 см.
- Если на правый поршень поместить груз массой
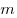 , то
пружина растянется на величину , то
пружина растянется на величину
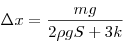 . .
- Отношение сил
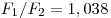 . .
- Потенциальная энергия воды увеличится за счет переноса вытесненной
камнем воды на поверхность.
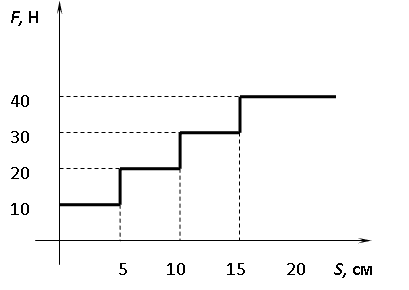
- Смотрите график.
- К верхнему динамометру приложена сила
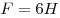 . .
- Показания среднего динамометра равны 60 Н. Масса динанометра равна
3 кг.
- Искомые массы суть
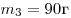 и и 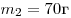 . .
- Объем алюминиевого куба равен 73,8 см3.
- Расстояние от потолка до нижнего шарика равно
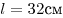 . .
- Давление в жидкости равно
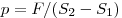 . .
- Плот выступает на высоту
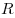 . .
- Решение задачи существует, когда либо
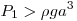 и
и 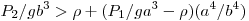 , либо , либо 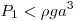 и и 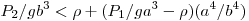 . В этих случаях находится в равновесии, если ее опора
расположена в точке . В этих случаях находится в равновесии, если ее опора
расположена в точке
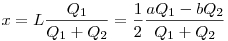 , где , где
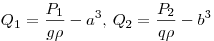 . .
- Скорость течения воды в трубке
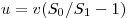 .
Вода начнет переливаться через верхний край трубки через .
Вода начнет переливаться через верхний край трубки через 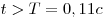 . .
- К концу 10-ой секунды весы будут показывать 15 г. Масса одной
бусинки равна 3 г. Объем одной бусинки равен
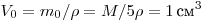 . .
- Гпафик силы натяжения от времени приведен на рисунке.
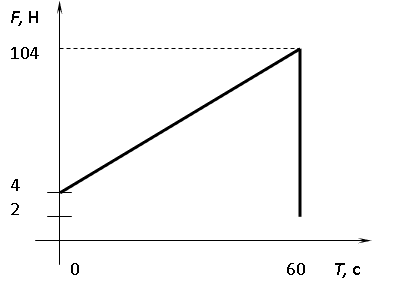
- Двигаясь по следу снегохода, человек будет проваливаться в снег.
- Шарик надо передвинуть на 10 см.
- Вода в трубке установится на высоте 3 м.
- Растяжение второй пружины равно 5 см.
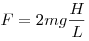 . .
- Чтобы чашка достала пола, на нее надо положить груз 1,3 кг.
Назад к задачам
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
|

