|
27. Масса. Плотность вещества
1. Однородные тела и их свойства. 2. Плотность, как макроскопическая характеристика веществ . 3. Плотность вещества и его строение. 4. Распространенные ошибки.
Из твердого вещества можно изготовить однородные тела. Свойство однородности состоит в следующем. Выделим в произвольно взятых точках тела иди наковые по массе части 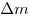 . Тело однородно, если объемы этих частей . Тело однородно, если объемы этих частей 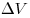 одинаковы. Из жидкости и газов также можно «изготовить» тела, заключив их в сосуды. одинаковы. Из жидкости и газов также можно «изготовить» тела, заключив их в сосуды.
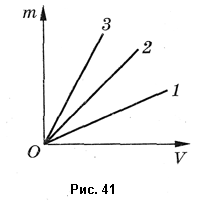
Для однородного тела можно выяснить зависимость массы от его объема. Эта зависимость будет линейной для любых веществ. Однако для разных веществ углы наклона соответствующих графиков к оси объемов различны (рис. 41). Следовательно, можно сделать вывод: отношение массы к объему для данно го вещества не зависит от объема, однако для разных веществ эти отношения различны. Например, дни графика 3 (см. рис. 41) это отношение больше, чем для графика 1.
Отношение 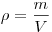 называется плотностью вещества. Единица плотности — кг/м3. называется плотностью вещества. Единица плотности — кг/м3.
Среди металлов маленькие плотности имеют калий, магний, литий. Наиболее легкий металл — литий — имеет плотность 534 кг/м3 (это меньше плотности воды). Металл с наибольшей плотностью — осмий. Его плотность 22 570 кг/м3.
Плотность вещества связана с его строением. Эта связь проявляется в том, что плотность равна
произведению концентрации частиц 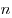 на массу на массу 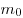 одной частицы
(молекулы, атома или иона) вещетва. Действительно, одной частицы
(молекулы, атома или иона) вещетва. Действительно, 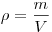 , однако , однако 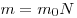 , где , где 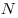 - общее число частиц. Итак, - общее число частиц. Итак, 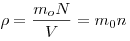 . .
твердых кристаллических веществ плотность может быть связана с периодом решетки 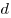 . .
Пусть вещество (например, медь) имеет кубическую гранецентрированную решетку (рис. 42). Тогда в объеме 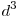 содержится 4 атома. Определим массу и объем этой ячейки. содержится 4 атома. Определим массу и объем этой ячейки.
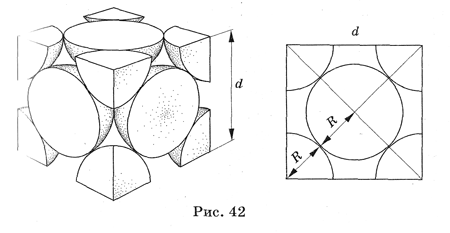
Если взять массу вещества, равную молярной массе 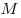 , то в ней содержится , то в ней содержится 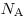 (число Авогадро) атомов. Следовательно, масса вещества в объеме (число Авогадро) атомов. Следовательно, масса вещества в объеме 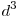 равна равна 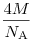 . Таким образом, плотность меди равна . Таким образом, плотность меди равна 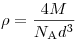 . .
Плотность газов легко изменяется, поэтому в разных изопроцессах она может изменяться. Это становится ясным, если уравнение Менделеева—Клапейрона записать, включив в него плотность. Действительно, 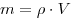 ; следовательно, ; следовательно, 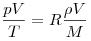 , или , или 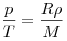 .
Отсюда можно сделать следующие выводы: .
Отсюда можно сделать следующие выводы:
1) при изотермическом процессе (Т = const) плотность газа пропорциональна давлению: 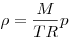 ; ;
2) при изобарном процессе (р = const) плотность газа обратно пропорциональна температуре: 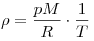 ; ;
3) понятно, что при изохорном процессе (V = const) плотность газа не изменяется.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
