Интерференция света
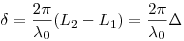
|
Разность фаз двух когерентных волн, где 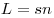 — оптическая длина пути (
— оптическая длина пути (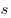 —
геометрическая
длина пути световой волны в среде, —
геометрическая
длина пути световой волны в среде,  —
показатель
преломления этой среды), —
показатель
преломления этой среды), 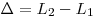 —
оптическая разность хода двух световых волн,
—
оптическая разность хода двух световых волн, 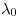 — длины волны в вакууме.
— длины волны в вакууме.
|
|
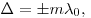
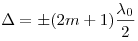
|
Условие интерференционных максимумов и минимумов
соответственно, где 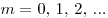 . .
|
|
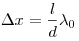
|
Ширина интерференционной полосы, где 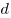 —
расстояние между двумя когерентными источниками,
находящимися на
расстоянии —
расстояние между двумя когерентными источниками,
находящимися на
расстоянии 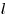 от экрана, параллельно обоим
источниками, при
условии от экрана, параллельно обоим
источниками, при
условии 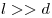 . .
|
|
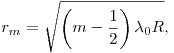
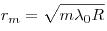
|
Радиусы светлых и темных колец Ньютона соответственно в
отраженном свете (или темных и светлых соответственно в
проходящем
свете), где  — номер кольца, — номер кольца, 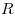 —
радиус кривизны линзы,
—
радиус кривизны линзы, 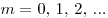 . .
|
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
|

