
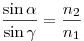
|
Законы отражения и преломления света, где 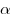 — угол падения,
— угол падения, 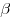 — угол отражения, — угол отражения,
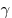 — угол преломления, — угол преломления,  — относительный показатель преломления второй среды
относительно первой, — относительный показатель преломления второй среды
относительно первой, 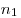 и и 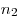 —
абсолютные показатели преломления первой и второй среды. —
абсолютные показатели преломления первой и второй среды.
|
|
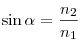
|
Предельный угол полного отражения при распространении света из
среды оптически более плотной в среду оптически менее плотную (угол
полного внутреннего отражения).
|
|
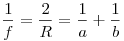
|
Формула сферического зеркала, где  и и  — соответственно расстояния от полюса зеркала до предмета и
изображения,
— соответственно расстояния от полюса зеркала до предмета и
изображения, 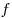 — фокусное расстояние зеркала, — фокусное расстояние зеркала,
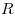 — радиус кривизны зеркала. — радиус кривизны зеркала.
|
|
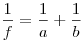
|
Формула тонкой линзы, где 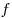 — фокусное
расстояние линзы, — фокусное
расстояние линзы,  и и  расстояния от оптического
центра линзы до предмета и изображения соответственно. расстояния от оптического
центра линзы до предмета и изображения соответственно.
|
|
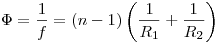
|
Оптическая сила тонкой линзы, где 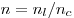 — относительный показатель преломления (
— относительный показатель преломления (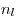 и и 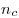 — абсолютные показатели преломления линзы и окружающей
среды соответственно), — абсолютные показатели преломления линзы и окружающей
среды соответственно), 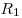 и и 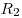 —
радиусы кривизны поверхностей ( —
радиусы кривизны поверхностей (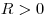 для выпуклой
поверхности, для выпуклой
поверхности, 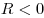 для вогнутой). для вогнутой).
|
|
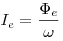
|
Сила излучения, где 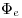 — поток
излучения источника, — поток
излучения источника, 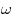 — телесный угол, в
пределах которого это излучение распространяется. — телесный угол, в
пределах которого это излучение распространяется.
|
|
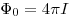
|
Полный световой поток, испускаемый изотропным точечным
источником, где 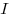 — сила света источника. — сила света источника.
|
|
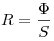
|
Светимость поверхности, где 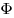 — световой
поток, испускаемый поверхностью, — световой
поток, испускаемый поверхностью,  — площадь этой
поверхности. — площадь этой
поверхности.
|
|
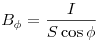
|
Яркость светящейся поверхности в некотором направлении
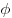 , где , где 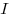 — сила света, — сила света,  — площадь поверхности,
— площадь поверхности, 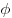 — угол между
нормалью к элементу поверхности и направлением наблюдения. — угол между
нормалью к элементу поверхности и направлением наблюдения.
|
|
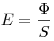
|
Освещенность поверхности, где 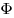 —
световой поток, падающих на поверхность, —
световой поток, падающих на поверхность,  — площадь
этой поверхности. — площадь
этой поверхности.
|
|
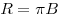
|
Связь светимости 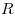 и яркости и яркости  при
условии, что яркость не зависит от направления. при
условии, что яркость не зависит от направления.
|

