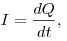
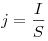
|
Сила 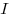 и плотность и плотность 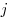 электрического
тока, где электрического
тока, где  — площадь поперечного сечения проводника, — площадь поперечного сечения проводника,
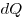 — заряд, протекающий через поперечное сечение
проводника за время — заряд, протекающий через поперечное сечение
проводника за время 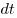 . .
|
|
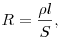
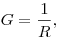
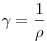
|
Сопротивление 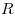 однородного линейного проводника,
проводимость однородного линейного проводника,
проводимость 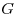 проводника и удельная электрическая
проводимость проводника и удельная электрическая
проводимость 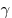 вещества проводника, где вещества проводника, где 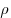 — удельное электрическое сопротивление, — удельное электрическое сопротивление,  — площадь поперечного сечения проводника,
— площадь поперечного сечения проводника, 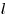 —
его длина. —
его длина.
|
|
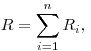
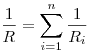
|
Сопротивление системы проводников при последовательном и
параллельном соединении соответственно, где 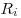 —
сопротивление —
сопротивление 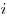 -того проводника, -того проводника,  — число
проводников. — число
проводников.
|
|
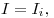
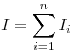
|
Сила тока системы проводников при последовательном и
параллельном соединении соответственно, где 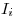 —
сила тока —
сила тока 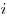 -того проводника, -того проводника,  — число
проводников. — число
проводников.
|
|
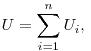

|
Напряжение системы проводников при последовательном и
параллельном соединении соответственно, где 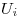 —напряжение на
—напряжение на 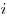 -том проводнике, -том проводнике,  —
число проводников. —
число проводников.
|
|
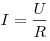
|
Закон Ома для однородного участка цепи.
|
|
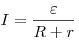
|
Закон Ома для замкнутой цепи, где 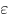 — э. д. с. источников тока цепи,
— э. д. с. источников тока цепи, 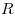 —
сопротивление цепи, —
сопротивление цепи, 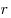 — внутреннее сопротивление
источника тока. — внутреннее сопротивление
источника тока.
|
|
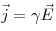
|
Закон Ома в дифференциальной форме, где 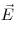 — напряженность электростатического поля,
— напряженность электростатического поля, 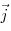 — плотность тока,
— плотность тока, 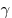 — удельная
проводимость. — удельная
проводимость.
|
|
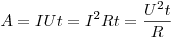
|
Работа электрического тока за время 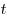 . .
|
|
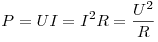
|
Мощность электрического тока.
|
|
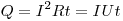
|
Закон Джоуля-Ленца, где 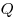 — количество
теплоты, выделяющееся на участке цепи за время — количество
теплоты, выделяющееся на участке цепи за время 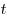 . .
|
|
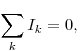
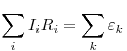
|
Правила Кирхгофа.
|

