Упругие деформации

|
Напряжение упругой деформации, где 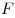 —
растягивающая (сжимающая) сила, —
растягивающая (сжимающая) сила,  —
площадь
поперечного сечения. —
площадь
поперечного сечения.
|
|

|
Относительное поперечное растяжение (сжатие), где
 — изменение длины тела, при растяжении
(сжатии), — изменение длины тела, при растяжении
(сжатии),
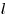 — длина тела до деформации. — длина тела до деформации.
|
|

|
Относительное продольное растяжение (сжатие), где
 — изменения диаметра стержня при растяжении
(сжатии), — изменения диаметра стержня при растяжении
(сжатии),
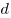 — диаметр стержня до деформации. — диаметр стержня до деформации.
|
|

|
Связь между относительным поперечным растяжением (сжатием)
 и относительным продольным
растяжением
(сжатием) и относительным продольным
растяжением
(сжатием) 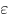 , где , где 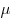 —
коэффициент Пуассона. —
коэффициент Пуассона.
|
|

|
Закон Гука для продольного растяжения (сжатия), где
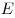 — модуль Юнга.
Или: — модуль Юнга.
Или:
 — удлинение стержня, — удлинение стержня, 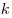 —
коэффициент упругости, —
коэффициент упругости, 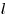 — длины стержня, — длины стержня,
 — площадь поперечного сечения.
— площадь поперечного сечения.
|
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
|

