Кинематика

|
Средняя скорость (вектор средней скорости) материальной точки
(частицы), где  — элементарное
перемещение
частицы за промежуток времени — элементарное
перемещение
частицы за промежуток времени  . .
|
|

|
Мгновенная скорость частицы, где  — радиус-вектор и — радиус-вектор и  —
координаты движущейся частицы,
—
координаты движущейся частицы,  — орты (единичные векторы) прямоугольной декартовой системы
координат,
— орты (единичные векторы) прямоугольной декартовой системы
координат,  , ,
 , ,  , ,  —
проекции скорости на оси прямоугольной декартовой системы
координат,
—
проекции скорости на оси прямоугольной декартовой системы
координат,
 . .
|
|

|
Путь, пройденный частицей за промежуток времени  , ,
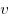 — модуль скорости — модуль скорости
|
|

|
Среднее ускорение частицы, где  — путь,
пройденный частицей за промежуток времени — путь,
пройденный частицей за промежуток времени  . .
|
|

|
Мгновенное ускорение частицы, где  , ,  , ,  , ,  — проекции ускорения на оси
прямоугольной
декартовой системы координат, — проекции ускорения на оси
прямоугольной
декартовой системы координат,  . .
|
|

|
Путь при равнопеременном движении, где  —
начальная скорость, а — ускорение, t —
время
движения. —
начальная скорость, а — ускорение, t —
время
движения.
|
|

|
Скорость при равнопеременном движении.
|

|
Закон сложения скоростей в механике, где  —
скорость тела относительно неподвижной системы отсчета
(абсолютная
скорость),
—
скорость тела относительно неподвижной системы отсчета
(абсолютная
скорость),  — скорость тела
относительно
подвижной системы отсчета (относительная скорость), — скорость тела
относительно
подвижной системы отсчета (относительная скорость),  — скорость подвижной системы относительно неподвижной
(переносная скорость). — скорость подвижной системы относительно неподвижной
(переносная скорость).
|
|

|
Угловая скорость твердого тела, где  —
угол поворота твердого тела вокруг неподвижной оси за промежуток
времени
—
угол поворота твердого тела вокруг неподвижной оси за промежуток
времени  . .
|
|

|
Связь между линейной скоростью 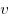 и угловой скоростью и угловой скоростью
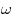 , R — расстояние от оси вращения.} , R — расстояние от оси вращения.}
|
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
|

