Московский Физико-Технический Институт
1997 год
Решите неравенство
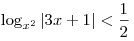 . .
Решите уравнение
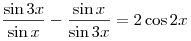 . .
Окружность касается
сторон 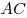 и и  треугольника треугольника  в
точках в
точках  и и  соответственно. На дуге этой
окружности, лежащей внутри треугольника, расположена точка соответственно. На дуге этой
окружности, лежащей внутри треугольника, расположена точка 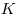 так, что расстояние от нее до сторон
так, что расстояние от нее до сторон 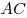 и и  равны
равны 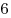 и и 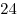 соответственно. Найдите расстояние
от точки соответственно. Найдите расстояние
от точки 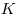 до стороны до стороны  . .
Графику функции 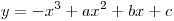 принадлежат точки принадлежат точки  и и
 , симметричные относительно прямой , симметричные относительно прямой 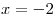 .
Касательные к этому графику в точках .
Касательные к этому графику в точках  и и  параллельны между собой. Одна из этих касательных проходит через точку
параллельны между собой. Одна из этих касательных проходит через точку
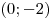 , а другая — через точку , а другая — через точку 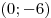 . Найдите значения . Найдите значения  , ,  и и 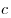 . .
Внутри цилиндра лежат два
шара радиуса 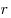 и один шар радиуса и один шар радиуса 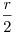 ,
так что каждый шар касается двух других, нижнего основания цилиндра и
его боковой поверхности. Найдите радиус основания цилиндра. ,
так что каждый шар касается двух других, нижнего основания цилиндра и
его боковой поверхности. Найдите радиус основания цилиндра.
2007 год
Решить уравнение
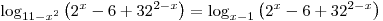 . .
Решите уравнение
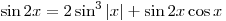 . .
Решите неравенство
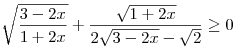 . .
Окружности 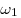 и и 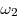 лежат внутри треугольника лежат внутри треугольника
 , в котором , в котором 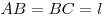 , , 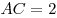 , а
радиус , а
радиус 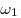 в два раза больше радиуса в два раза больше радиуса 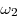 . Окружности . Окружности 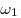 и и 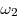 касаются внешним образом, причем
касаются внешним образом, причем 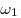 касается сторон касается сторон
 и и 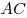 , а , а 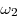 — сторон — сторон  и и 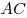 треугольника
треугольника  . Найти радиус окружности . Найти радиус окружности 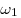 , если , если 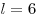 . Найти все значения . Найти все значения 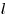 , при
которых существуют указанные окружности. , при
которых существуют указанные окружности.
Найти все значения
параметра  , при которых наибольшее значение величины , при которых наибольшее значение величины
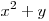 на множестве пар действительных чисел на множестве пар действительных чисел
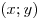 , удовлетворяющих одновременно двум неравенствам , удовлетворяющих одновременно двум неравенствам 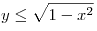 и и  , будет максимально возможным. Найти это максимально возможное
значение. , будет максимально возможным. Найти это максимально возможное
значение.
В прямоугольном
параллелепипеде 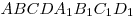 четыре
числа — длины ребер и диагонали четыре
числа — длины ребер и диагонали 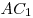 — образуют арифметическую прогрессию с
положительной разностью — образуют арифметическую прогрессию с
положительной разностью 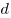 , причем , причем 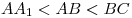 . Две внешне касающиеся друг друга сферы одинакового
неизвестного радиуса . Две внешне касающиеся друг друга сферы одинакового
неизвестного радиуса 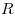 расположены так, что их центры лежат
внутри параллелепипеда, причем первая сфера касается граней расположены так, что их центры лежат
внутри параллелепипеда, причем первая сфера касается граней 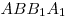 , , 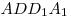 , , 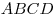 , а
вторая — граней , а
вторая — граней 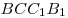 , , 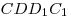 , , 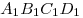 . Найти: а) длины ребер
параллелепипеда, б) угол между прямыми . Найти: а) длины ребер
параллелепипеда, б) угол между прямыми 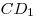 и и 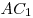 , в) радиус , в) радиус 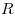 . .
Ответы
2007 год
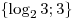 . .
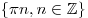 , , 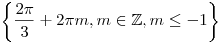 , , 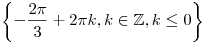 . .
-
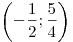 . .
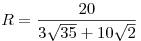 , , 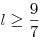 . .
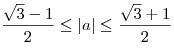 ; ;
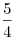 . .
- а)
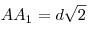 , , 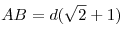 ; б) ; б)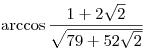 ;
в) ;
в) 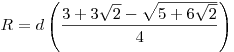 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
|

