Санкт-Петербургский Государственный Унивеситет
Геологический факультет
1977 год
Решить неравенство
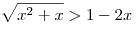 . .
Найти все решения
уравнения 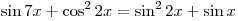 ,
лежащие в интервале ,
лежащие в интервале 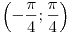 . .
Решить уравнение
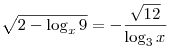 . .
Вычислить площадь
криволинейного треугольника, лежащего в первой четверти и ограниченного
линиями 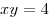 , , 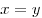 , , 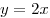 . .
Вектор
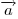 , коллинеарный вектору , коллинеарный вектору
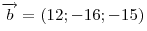 , образует с осью , образует с осью
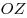 острый угол. Зная, что острый угол. Зная, что 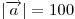 , найти его координаты. , найти его координаты.
Ответы
1997 год
По окружности радиуса
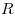 движутся в одинаковом направлении две материальные точки
со скоростями движутся в одинаковом направлении две материальные точки
со скоростями 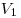 и и 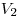 . Найдите расстояние
между ними через время . Найдите расстояние
между ними через время 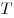 , если известно, что они начали свое
движение одновременно из диаметрально противоположных точек. , если известно, что они начали свое
движение одновременно из диаметрально противоположных точек.
а) Решите уравнение
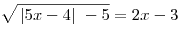 (кроме геологического
факультета). (кроме геологического
факультета).
б) Решите уравнение 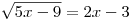 (геологический факультет). (геологический факультет).
Решите уравнение
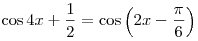 . .
Нарисуйте график функции
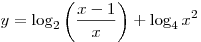 . .
Отрезок  является гипотенузой прямоугольного треугольника
является гипотенузой прямоугольного треугольника  и
стороной равностороннего треугольника и
стороной равностороннего треугольника 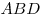 . Найдите отношение . Найдите отношение
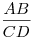 , если известно, что , если известно, что 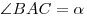 и что отрезки и что отрезки  и и 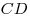 не
пересекаются. не
пересекаются.
Ответы
2007 год
Из некоторого пункта
выехали велосипед и через 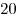 минут вслед за ним автомобиль и
мотоцикл. Автомобиль, догнав велосипед, мгновенно повернул обратно и
спустя минут вслед за ним автомобиль и
мотоцикл. Автомобиль, догнав велосипед, мгновенно повернул обратно и
спустя 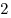 минуты встретил мотоцикл. Скорости мотоцикла и
велосипеда равны минуты встретил мотоцикл. Скорости мотоцикла и
велосипеда равны 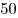 и и 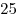 км/ч. Найти скорость автомобиля. км/ч. Найти скорость автомобиля.
Решить уравнение
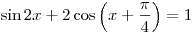 . .
Решить уравнение
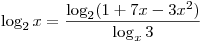 . .
В окружность радиуса
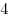 вписан прямоугольный треугольник площади вписан прямоугольный треугольник площади 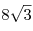 . Биссектрисы углов треугольника пересекают эту окружность с
точках . Биссектрисы углов треугольника пересекают эту окружность с
точках  , ,  и и  . Найти площадь
треугольника . Найти площадь
треугольника  . .
Изобразить на плоскости
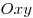 множество точек, координаты которых удовлетворяют
равенству множество точек, координаты которых удовлетворяют
равенству 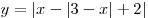 . .
Ответы
Ответы
1977 год
-
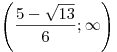 . .
-
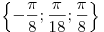 . .
-
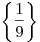 . .
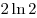 . .
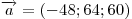 . .
1997 год
- искомое расстояние
равно
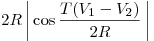 . .
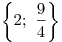 . .
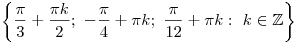 . .
-
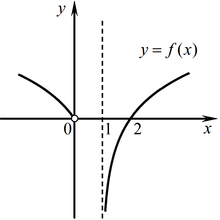
-
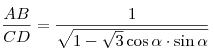 . .
2007 год
- Скорость автомобиля равна
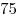 км/ч или км/ч или 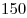 км/ч. км/ч.
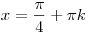 , , 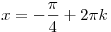 , , 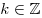 . .
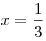 , , 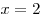 . .
- Площадь треугольника
 равна равна 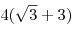 . .
-
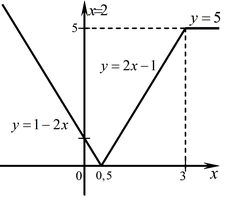
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
|

