Московский государственный университет им. М.В. Ломоносова
Механико-математический факультет
1977 год
-
Решить неравенство
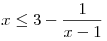 . .
Длины боковых сторон
трапеции равны 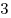 и и 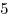 . Известно, что в трапецию
можно вписать окружность. Средняя линия трапеции делит ее на две части,
отношение площадей которых равно . Известно, что в трапецию
можно вписать окружность. Средняя линия трапеции делит ее на две части,
отношение площадей которых равно 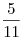 . Найти длины
оснований трапеции. . Найти длины
оснований трапеции.
-
Решить уравнение 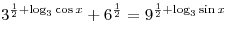 . .
Решить систему уравнений
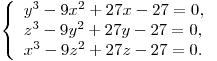
Основанием пирамиды
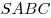 является равносторонний треугольник является равносторонний треугольник  ,
длина стороны которого равна ,
длина стороны которого равна 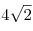 . Боковое ребро . Боковое ребро
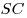 перпендикулярно плоскости основания и имеет длину перпендикулярно плоскости основания и имеет длину
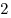 . Найти величину угла и расстояние между скрещивающимися
прямыми, одна из которых проходит через точку . Найти величину угла и расстояние между скрещивающимися
прямыми, одна из которых проходит через точку  и середину
ребра и середину
ребра  , а другая проходит через точку , а другая проходит через точку 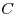 и
середину ребра и
середину ребра  . .
Ответы
1997 год
Решить уравнение 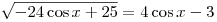 . .
Решить
неравенство 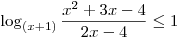 . .
Считая  и и
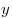 целыми числами, решить систему уравнений целыми числами, решить систему уравнений
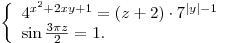
В окружности
проведены хорды 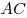 и и 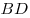 , пересекающиеся в точке , пересекающиеся в точке
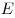 , причем касательная к окружности, проходящая через точку , причем касательная к окружности, проходящая через точку
 параллельна параллельна 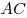 . Известно, что . Известно, что 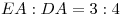 , а площадь треугольника , а площадь треугольника 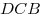 равна 16. Найти
площадь треугольника равна 16. Найти
площадь треугольника 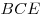 . .
Решить систему
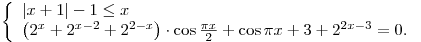
В кубе 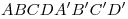 длина ребра равна 1. Одна сфера радиуса
длина ребра равна 1. Одна сфера радиуса 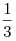 касается
плоскости касается
плоскости  в точке в точке  , другая сфера касается
плоскости , другая сфера касается
плоскости 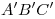 в точке в точке 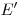 , лежащей на отрезке , лежащей на отрезке
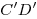 , причем , причем 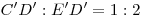 . Известно, что эти
сферы касаются друг друга внешним образом и точка их касания лежит
внутри куба. Найти расстояние от точки касания сфер до точки . Известно, что эти
сферы касаются друг друга внешним образом и точка их касания лежит
внутри куба. Найти расстояние от точки касания сфер до точки
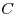 . .
Ответы
2007 год
Учитель назвал Пете
натуральное число и попросил найти сумму его логарифмов по основаниям
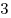 и и 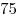 . Однако Петя, по ошибке, не сложил эти
логарифмы, а перемножил их, получив неверный ответ, который оказался
вдвое меньше верного. Какое число назвал ему учитель? . Однако Петя, по ошибке, не сложил эти
логарифмы, а перемножил их, получив неверный ответ, который оказался
вдвое меньше верного. Какое число назвал ему учитель?
Графики функций
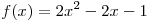 и и 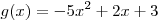 пересекаются в двух точках. Найти коэффициенты
пересекаются в двух точках. Найти коэффициенты  и и
 в уравнении прямой в уравнении прямой 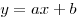 , проходящей через
те же точки. , проходящей через
те же точки.
Решить уравнение
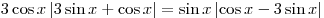 . .
Точки 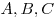 лежат на окружности радиуса
лежат на окружности радиуса 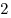 с центром с центром 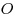 , а
точка , а
точка 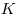 — на прямой, касающейся этой
окружности в точке — на прямой, касающейся этой
окружности в точке  , причем , причем 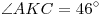 , а длины отрезков , а длины отрезков 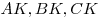 образуют возрастающую
геометрическую прогрессию (в указанном порядке). Найти угол образуют возрастающую
геометрическую прогрессию (в указанном порядке). Найти угол 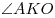 и расстояние между точками и расстояние между точками  и и 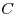 . Какой
из углов больше . Какой
из углов больше 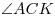 или или 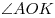 ? ?
Найти наибольшее
значение выражения 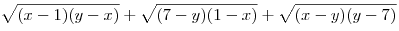 при при ![x \in \left[ { - 2;3}
\right] x \in \left[ { - 2;3}
\right]](/inc/pictures/9c7e24fa035c9157b4e3c12f02e6a328.png) и и ![y \in \left[ {0;11} \right] y \in \left[ {0;11} \right]](/inc/pictures/0a6d4376ae49918392f9ce40f969347e.png) . .
Два конуса имеют общую
вершину, и единственную общую образующую, которая составляет с их осями
углы в 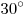 и и 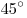 . Двугранный угол
расположен так, что каждая его грань касается каждого из конусов по
разным образующим. Найти величину этого угла. . Двугранный угол
расположен так, что каждая его грань касается каждого из конусов по
разным образующим. Найти величину этого угла.
Ответы
Ответы
1977 год
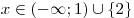 . .
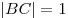 , , 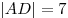 . .
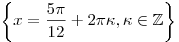 . .
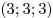 . .
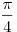 , , 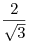 . .
1997 год
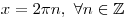 . .
-
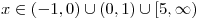 . .
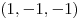 , , 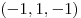 . .
- 9.
- 2.
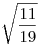 . .
2007 год
-
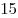 . .
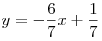 . .
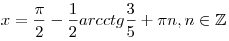 . .
-
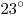 , , 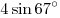 , одинаковы. , одинаковы.
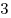 . .
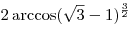 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
|

