Последние новости науки

Приз в 1 миллион долларов за решение каждой из семи математических проблем
(по материалам сайта http://www.claymath.org./prize_problems/index.htm)

      CMI — The Clay Mathematics Institute (Кембридж, Штат Массачусетс) — назвал семь нерешенных математических проблем — «Millennium Prize Problems», за решение каждой из которых будет выплачен $1 млн. К рассмотрению принимаются решения, которые были опубликованы в известном математическом журнале, причем не ранее, чем через 2 года после публикации (для всестороннего рассмотрения математическим сообществом).

      Перечислим эти проблемы:

      Проблема Кука (сформулирована в 1971г.).
      Допустим, находясь в большой компании, Вы хотите убедиться, что там же находится Ваш знакомый. Если Вам скажут, что он сидит в углу, то Вам достаточно доли секунды, чтобы, бросив взгляд, убедиться в истинности информации. В отсутствии этой информации Вы будете вынуждены обойти всю комнату, рассматривая гостей.
      Точно так же, если кто-то сообщит Вам, что число 13717421 можно представить, как произведение двух меньших чисел, непросто быстро убедиться в истинности информации, но если Вам сообщат, что исходное число можно разложить на множители 3607 и 3803, то это утверждение легко проверяется с помощью калькулятора.
      Это примеры иллюстрируют общее явление: решение какой-либо задачи часто занимает больше времени, чем проверка правильности решения. Стивен Кук сформулировал проблему: может ли проверка правильности решения задачи быть более длительной, чем само получение решения, независимо от алгоритма проверки.
      Эта проблема является одной из нерешенных проблем логики и информатики. Ее решение могло бы революционным образом изменить основы криптографии, используемой при передаче и хранении данных.

      Гипотеза Римана (сформулирована в 1859г.).
      Некоторые целые числа не могут быть выражены как произведение двух меньших целых чисел, например, 2, 3, 5, 7, и т.д. Такие числа называются простыми числами, и они играют важную роль в чистой математике и ее приложениях. Распределение простых чисел среди всех натуральных чисел не подчиняется никакой закономерности, однако немецкий математик Риман (1826-1866) обнаружил, что число простых чисел, не превосходящих , выражается через распределение нетривиальных нулей дзета-функции Римана. Риман высказал гипотезу, не доказанную и не опровергнутую до сих пор, что все нетривиальные нули дзета-функции лежат на прямой линии. На сегодняшний день проверены первые 1500000000 решений.

      Гипотеза Берча и Свиннертон-Дайера.
      Математики давно заворожены проблемой описания всех решений в целых числах , , 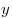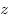алгебраических уравнений, то есть уравнений от нескольких переменных с целыми коэффициентами. Примером алгебраического уравнения является уравнение 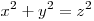. Евклид дал полное описание решений этого уравнения, но для более сложных уравнений получение решения становится чрезвычайно трудным (например, доказательство отсутствия целых решений уравнения ).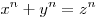
      В 1970 г. Юрий Владимирович Матиясевич дал отрицательное решение десятой проблемы Гильберта, т.е. не имеется никакого алгоритма, с помощью которого можно было бы узнать, разрешимо уравнение в целых числах или нет. Но в частном случае, когда решения образуют абелево многообразие, Берч и Свиннертон-Дайер предположили, что число решений определяется значением связанной с уравнением дзета-функции в точке 1: если значение дзета-функции в точке 1 равно 0, то имеется бесконечное число решений, и наоборот, если не равно 0, то имеется только конечное число таких решений.

      Гипотеза Ходжа.
      В двадцатом веке математики изобрели мощные методы исследования формы сложных объектов. Основная идея состоит в том, чтобы выяснить, до какой степени мы можем аппроксимировать форму данного объекта, склеивая вместе простые тела возрастающей размерности. Этот метод оказался эффективным при описании разнообразных объектов встречающихся в математике. К сожалению, при этом были не ясны геометрические обоснования метода: в некоторых случаях было необходимо прибавлять части, которые не имели никакого геометрического истолкования.
      Гипотеза Ходжа состоит в том, что для особенно хороших типов пространств, называемых проективными алгебраическими многообразиями, т.н. циклы Ходжа являются комбинациями объектов, имеющих геометрическую интерпретацию, — алгебраических циклов.

      Уравнения Навье-Стокса.
      Если плыть в лодке по озеру, то возникнут волны, а если лететь в самолете — в воздухе возникнут турбулентные потоки. Предполагается, что эти и другие явления описываются уравнениями, известными как уравнения Навье-Стокса. Решения этих уравнений не известны, и при этом даже не известно, как их решать. Необходимо показать, что решение существует и является достаточно гладкой функцией. Решение этой проблемы позволит существенно изменить способы проведения гидро- и аэродинамических расчетов.

      Проблема Пуанкаре.
      Если натянуть резиновую ленту на яблоко, то можно, медленно перемещая ленту без отрыва от поверхности, сжать ее до точки. С другой стороны, если ту же самую резиновую ленту соответствующим образом натянуть вокруг бублика, то никаким способом невозможно сжать ленту в точку, не разрывая ленту или не ломая бублик. Говорят, что поверхность яблока «односвязна», а поверхность бублика — нет. Пуанкаре почти сто лет назад знал, что в двумерном случае односвязна только сфера, и задался аналогичным вопросом для трехмерной сферы — множества точек в четырехмерном пространстве, равноудаленных от некоторой точки. Доказать, что односвязна только сфера, оказалось настолько трудно, что математики до сих пор ищут ответ.

      Уравнения Янга-Миллса.
      Уравнения квантовой физики описывают мир элементарных частиц. Почти пятьдесят лет назад, физики Янг и Миллс, обнаружив связь между геометрией и физикой элементарных частиц, написали свои уравнения. Тем самым они нашли путь к объединению теорий электромагнитного, слабого и сильного взаимодействий. Из уравнений Янга-Миллса следовало существование частиц, которые действительно наблюдались в лабораториях во всем мире, включая Brookhaven, Stanford, и CERN. Поэтому калибровочная теория Янга-Миллса принята большинством физиков, несмотря на то, что в рамках этой теории до сих пор не удается предсказывать массы элементарных частиц.