|
МЕЖДУНАРОДНАЯ ДИСТАНЦИОННАЯ МАТЕМАТИЧЕСКАЯ ОЛИМПИАДА «ТРЕТЬЕ ТЫСЯЧЕЛЕТИЕ»
2007 год
Задачи для 5 класса
Лугопарк имеет форму квадрата 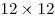 км, разбитого на три полосы, шириной по 4 км. Одна из крайних полос покрыта снегом, другая — песком, а на средней полосе залит каток. Конькобежец бежит по льду со скоростью 12 км/ч, по снегу
4 км/ч, а по песку — 3 км/ч. Лыжник бежит по льду со скоростью 3 км/ч, по снегу 12 км/ч, а по песку — 4 км/ч. Атлет бежит по льду со скоростью 4 км/ч, по снегу 3 км/ч, а по песку — 12 км/ч. Все трое одновременно стартуют из одного угла лугопарка, чтобы финишировать в противоположном. Каждый из них самостоятельно выбирает наиболее быстрый для себя маршрут движения. Кто из них прибежит первым? км, разбитого на три полосы, шириной по 4 км. Одна из крайних полос покрыта снегом, другая — песком, а на средней полосе залит каток. Конькобежец бежит по льду со скоростью 12 км/ч, по снегу
4 км/ч, а по песку — 3 км/ч. Лыжник бежит по льду со скоростью 3 км/ч, по снегу 12 км/ч, а по песку — 4 км/ч. Атлет бежит по льду со скоростью 4 км/ч, по снегу 3 км/ч, а по песку — 12 км/ч. Все трое одновременно стартуют из одного угла лугопарка, чтобы финишировать в противоположном. Каждый из них самостоятельно выбирает наиболее быстрый для себя маршрут движения. Кто из них прибежит первым?
У Вовы есть чудо-калькулятор с двумя кнопками, одна из которых увеличивает высвеченное на индикации число на 1, а другая — в 2 раза. В начальный момент на индикации 0. Помогите ему так нажать на эти кнопки, чтобы получить на индикации 2007. Как это сделать наименьшим числом нажатий?
В понедельник, среду и пятницу акции ООО «Рога и Копыта» росли в цене на 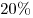 , а во вторник и четверг падали на , а во вторник и четверг падали на 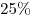 . В какой момент недели курс акций был выше
всего? . В какой момент недели курс акций был выше
всего?
Катя нашла наименьшее из натуральных чисел, у которых сумма цифр равна 2007. Чему равна сумма цифр следующего за ним числа?
Материки зеленой планеты занимают на ней вдвое большую площадь, чем океаны. Четверть площади материков занимают озера. Пятую часть площади океанов и шестую часть площади озер занимают острова. Чего больше на поверхности зеленой планеты — суши или воды?
Два игрока по очереди ставят цифры в свободные клетки квадрата 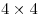 . Тот, кто ставит первую цифру, стремится сделать так, чтобы в каждой строчке, каждом столбце и каждом угловом квадрате . Тот, кто ставит первую цифру, стремится сделать так, чтобы в каждой строчке, каждом столбце и каждом угловом квадрате 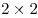 все 4 цифры оказались различными. Второй старается ему в этом помешать, однако не имеет права нарушать эти правила до тех пор, пока остается иная возможность. Кто из них достигнет своей цели, если будет действовать наилучшим образом? все 4 цифры оказались различными. Второй старается ему в этом помешать, однако не имеет права нарушать эти правила до тех пор, пока остается иная возможность. Кто из них достигнет своей цели, если будет действовать наилучшим образом?
Задачи для 6 класса
Лугопарк имеет форму квадрата 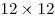 км, разбитого на три полосы, шириной по 4 км. Одна из крайних полос покрыта снегом, другая — песком, а на средней полосе залит каток. Конькобежец бежит по льду со скоростью 12 км/ч, по снегу 4 км/ч, а по песку — 3 км/ч. Лыжник бежит по льду со скоростью 3 км/ч, по снегу 12 км/ч, а по песку — 4 км/ч. Атлет бежит по льду со скоростью 4 км/ч, по снегу 3 км/ч, а по песку — 12 км/ч. Все трое одновременно стартуют из
одного угла лугопарка, чтобы финишировать в противоположном. Каждый из
них самостоятельно выбирает наиболее быстрый для себя маршрут движения.
Кто из них прибежит первым? км, разбитого на три полосы, шириной по 4 км. Одна из крайних полос покрыта снегом, другая — песком, а на средней полосе залит каток. Конькобежец бежит по льду со скоростью 12 км/ч, по снегу 4 км/ч, а по песку — 3 км/ч. Лыжник бежит по льду со скоростью 3 км/ч, по снегу 12 км/ч, а по песку — 4 км/ч. Атлет бежит по льду со скоростью 4 км/ч, по снегу 3 км/ч, а по песку — 12 км/ч. Все трое одновременно стартуют из
одного угла лугопарка, чтобы финишировать в противоположном. Каждый из
них самостоятельно выбирает наиболее быстрый для себя маршрут движения.
Кто из них прибежит первым?
У Миши есть чудо-калькулятор с двумя кнопками, одна из которых увеличивает высвеченное на индикации число на 1, а другая — в 3 раза. В начальный момент на индикации 0. Помогите ему так нажать на эти кнопки, чтобы получить на индикации 2007. Как это сделать наименьшим числом нажатий?
<> В понедельник, среду и пятницу акции ООО «Рога и Копыта» росли в цене на 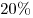 , а во вторник и четверг падали на , а во вторник и четверг падали на 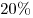 . В какой момент недели курс акций был выше всего? . В какой момент недели курс акций был выше всего?
Таня последовательно выписывает натуральные числа [Unparseable or potentially dangerous latex formula. Error 1 ]. Тот, кто ставит первую цифру, может ставить только нечетные цифры. Он стремится сделать так, чтобы в каждой строчке, каждом столбце и каждом угловом квадрате 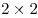 все 4 цифры оказались различными. Второй может ставить только четные цифры и старается помешать первому. Однако он не имеет права нарушать названные правила до тех пор, пока остается иная возможность. Кто из них достигнет своей цели, если будет действовать наилучшим образом? все 4 цифры оказались различными. Второй может ставить только четные цифры и старается помешать первому. Однако он не имеет права нарушать названные правила до тех пор, пока остается иная возможность. Кто из них достигнет своей цели, если будет действовать наилучшим образом?
Задачи для 7 класса
Лугопарк имеет форму квадрата 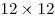 км, разбитого на три полосы, шириной по 4 км. Одна из крайних полос покрыта снегом, другая — песком, а на средней полосе залит каток. Конькобежец бежит по льду со скоростью 12 км/ч, по снегу 4 км/ч, а по песку — 3 км/ч. Лыжник бежит по льду со скоростью 3 км/ч, по снегу 12 км/ч, а по песку — 4 км/ч. Атлет бежит по льду со скоростью 4 км/ч, по снегу 3 км/ч, а по песку — 12 км/ч. Все трое одновременно стартуют из
одного угла лугопарка, чтобы финишировать в противоположном. Каждый из
них самостоятельно выбирает наиболее быстрый для себя маршрут движения.
Кто из них прибежит первым? км, разбитого на три полосы, шириной по 4 км. Одна из крайних полос покрыта снегом, другая — песком, а на средней полосе залит каток. Конькобежец бежит по льду со скоростью 12 км/ч, по снегу 4 км/ч, а по песку — 3 км/ч. Лыжник бежит по льду со скоростью 3 км/ч, по снегу 12 км/ч, а по песку — 4 км/ч. Атлет бежит по льду со скоростью 4 км/ч, по снегу 3 км/ч, а по песку — 12 км/ч. Все трое одновременно стартуют из
одного угла лугопарка, чтобы финишировать в противоположном. Каждый из
них самостоятельно выбирает наиболее быстрый для себя маршрут движения.
Кто из них прибежит первым?
У Бори есть чудо-калькулятор с двумя кнопками, одна из которых вычитает высвеченное на индикации число из 1, а другая — увеличивает в 2 раза. В начальный момент на индикации 0. Помогите ему так нажать на эти кнопки, чтобы получить на индикации 2007. Как это сделать наименьшим числом нажатий?
В понедельник, среду и пятницу акции ООО «Рога и Копыта» росли в цене на 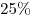 , а во вторник и четверг падали на , а во вторник и четверг падали на 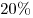 . В какой момент недели курс акций был выше всего? . В какой момент недели курс акций был выше всего?
Можно ли так раскрасить клетки квадрата 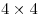 в 7 цветов, чтобы никакая пара цветов не встречалась в соседних клетках (имеющих общую сторону) более одного раза? в 7 цветов, чтобы никакая пара цветов не встречалась в соседних клетках (имеющих общую сторону) более одного раза?
Эскалатор на «Пушкинской» поднимает неподвижно стоящего пассажира за 120 секунд, а на «Пролетарской» за 140 секунд. Юра пробегает вверх по эскалатору на «Пушкинской» за 30 секунд, а Боря на
«Пролетарской» за 38 секунд. Кто из мальчиков бегает быстрее и во сколько раз?
Два игрока по очереди ставят цифры в свободные клетки квадрата 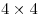 . Тот, кто ставит первую цифру, может ставить только цифры 1 или 3. Он стремится сделать так, чтобы в каждой строчке, каждом столбце и каждом угловом квадрате . Тот, кто ставит первую цифру, может ставить только цифры 1 или 3. Он стремится сделать так, чтобы в каждой строчке, каждом столбце и каждом угловом квадрате 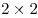 все 4 цифры оказались различными. Второй может ставить только цифры 2 или 4 и старается помешать первому. Однако он не имеет права нарушать названные правила до тех пор, пока остается иная возможность. Кто из них достигнет своей цели, если будет действовать наилучшим образом? все 4 цифры оказались различными. Второй может ставить только цифры 2 или 4 и старается помешать первому. Однако он не имеет права нарушать названные правила до тех пор, пока остается иная возможность. Кто из них достигнет своей цели, если будет действовать наилучшим образом?
Задачи для 8 класса
Лугопарк имеет форму квадрата 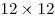 км, разбитого на три полосы, шириной по 4 км. Одна из крайних полос покрыта снегом, другая — песком, а на средней полосе залит каток. Конькобежец бежит по льду со скоростью 12 км/ч, по снегу 4 км/ч, а по песку — 3 км/ч. Лыжник бежит по льду со скоростью 3 км/ч, по снегу
12 км/ч, а по песку — 4 км/ч. Атлет бежит по льду со скоростью 4 км/ч, по снегу 3 км/ч, а по песку — 12 км/ч. Все трое одновременно стартуют из
одного угла лугопарка, чтобы финишировать в противоположном. Каждый из
них самостоятельно выбирает наиболее быстрый для себя маршрут движения.
Кто из них прибежит первым? км, разбитого на три полосы, шириной по 4 км. Одна из крайних полос покрыта снегом, другая — песком, а на средней полосе залит каток. Конькобежец бежит по льду со скоростью 12 км/ч, по снегу 4 км/ч, а по песку — 3 км/ч. Лыжник бежит по льду со скоростью 3 км/ч, по снегу
12 км/ч, а по песку — 4 км/ч. Атлет бежит по льду со скоростью 4 км/ч, по снегу 3 км/ч, а по песку — 12 км/ч. Все трое одновременно стартуют из
одного угла лугопарка, чтобы финишировать в противоположном. Каждый из
них самостоятельно выбирает наиболее быстрый для себя маршрут движения.
Кто из них прибежит первым?
У Коли есть чудо-калькулятор с двумя кнопками, одна из которых вычитает высвеченное на индикации число из 1, а другая — увеличивает в 3 раза. В начальный момент на индикации 0. Помогите ему так нажать на эти кнопки, чтобы получить на индикации 2007. Как это сделать наименьшим числом нажатий?
Галя последовательно выписывает натуральные числа в двоичной системе счисления 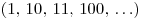 , суммирует записанные единицы и проверяет, не окажется ли сумма равной 2007. На каком числе Галя остановится, и что покажет ее проверка? , суммирует записанные единицы и проверяет, не окажется ли сумма равной 2007. На каком числе Галя остановится, и что покажет ее проверка?
Найдите такие натуральные  и и  , что , что 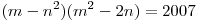 . .
Эскалатор на «Пушкинской» поднимает неподвижно стоящего пассажира за 120 секунд, а на «Пролетарской» за 140 секунд. Юра пробегает вверх по эскалатору на «Пушкинской» за 30 секунд, а Вася на
«Пролетарской» за 40 секунд. Кто из мальчиков бегает быстрее и на сколько процентов?
Два игрока по очереди ставят цифры от 1 до 4 в свободные клетки квадрата 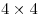 . Тот, кто ставит первую цифру, стремится сделать так, чтобы в каждой строчке, каждом столбце и каждом угловом квадрате . Тот, кто ставит первую цифру, стремится сделать так, чтобы в каждой строчке, каждом столбце и каждом угловом квадрате 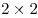 все 4 цифры оказались различными. Второй старается помешать первому. Однако он не имеет права нарушать названные правила до тех пор, пока остается иная возможность. Кто из них достигнет своей цели, если будет действовать наилучшим образом? все 4 цифры оказались различными. Второй старается помешать первому. Однако он не имеет права нарушать названные правила до тех пор, пока остается иная возможность. Кто из них достигнет своей цели, если будет действовать наилучшим образом?
Задачи для 9 класса
Лугопарк имеет форму квадрата 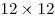 км, разбитого на три полосы, шириной по 4 км. Одна из крайних полос покрыта снегом, другая — песком, а на средней полосе залит каток. Конькобежец бежит по льду со скоростью 12 км/ч, по снегу 4 км/ч, а по песку — 3 км/ч. Лыжник бежит по льду со скоростью 3 км/ч, по снегу 12 км/ч, а по песку — 4 км/ч. Атлет бежит по льду со скоростью 4 км/ч, по снегу 3 км/ч, а по песку — 12 км/ч. Все трое одновременно стартуют из
одного угла лугопарка, чтобы финишировать в противоположном. Каждый из
них самостоятельно выбирает наиболее быстрый для себя маршрут движения.
Кто из них прибежит первым? км, разбитого на три полосы, шириной по 4 км. Одна из крайних полос покрыта снегом, другая — песком, а на средней полосе залит каток. Конькобежец бежит по льду со скоростью 12 км/ч, по снегу 4 км/ч, а по песку — 3 км/ч. Лыжник бежит по льду со скоростью 3 км/ч, по снегу 12 км/ч, а по песку — 4 км/ч. Атлет бежит по льду со скоростью 4 км/ч, по снегу 3 км/ч, а по песку — 12 км/ч. Все трое одновременно стартуют из
одного угла лугопарка, чтобы финишировать в противоположном. Каждый из
них самостоятельно выбирает наиболее быстрый для себя маршрут движения.
Кто из них прибежит первым?
В треугольник, длины всех сторон которого измеряются целыми числами, вписан круг радиуса 1. Достаточно ли этой информации для нахождения длин сторон?
Катя нашла наименьшее из натуральных чисел, у которых сумма цифр равна 2007. Чему равна сумма цифр следующего за ним числа?
Найдите такие натуральные  и и  , что , что 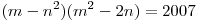 . .
В момент, когда Аня и Ира зашли на встречные эскалаторы, они оказались на ступеньках под одинаковыми номерами. Затем обе девочки шагали по ходу движения и в момент схода они снова оказались на ступеньках под одинаковыми номерами. Ступеньки обоих эскалаторов занумерованы снизу вверх (после последнего номера идет первый). Могло ли еще один раз произойти совпадение номеров ступенек, на которых в тот момент находились Аня и Ира?
Два игрока по очереди ставят цифры от 1 до 9 в свободные клетки квадрата 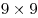 . Тот, кто ставит первую цифру, может ставить только нечетные цифры. Он стремится сделать так, чтобы в каждой строчке, каждом столбце и каждом из 9 квадратов . Тот, кто ставит первую цифру, может ставить только нечетные цифры. Он стремится сделать так, чтобы в каждой строчке, каждом столбце и каждом из 9 квадратов 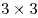 , на которые разбивается основной квадрат, все 9 цифр оказались различными. Второй может ставить только четные цифры или 9. Он старается помешать первому, однако не имеет права нарушать названные правила до тех пор, пока остается иная возможность. Кто из них достигнет своей цели, если будет действовать наилучшим образом? , на которые разбивается основной квадрат, все 9 цифр оказались различными. Второй может ставить только четные цифры или 9. Он старается помешать первому, однако не имеет права нарушать названные правила до тех пор, пока остается иная возможность. Кто из них достигнет своей цели, если будет действовать наилучшим образом?
Задачи для 10 класса
Лугопарк имеет форму квадрата 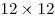 км, разбитого на три полосы, шириной по 4 км. Одна из крайних полос покрыта снегом, другая — песком, а на средней полосе залит каток. Конькобежец бежит по льду со скоростью 12 км/ч, по снегу 4 км/ч, а по песку — 3 км/ч. Лыжник бежит по льду со скоростью 3 км/ч, по снегу
12 км/ч, а по песку — 4 км/ч. Атлет бежит по льду со скоростью 4 км/ч, по снегу 3 км/ч, а по песку — 12 км/ч. Все трое одновременно стартуют из
одного угла лугопарка, чтобы финишировать в противоположном. Каждый из
них самостоятельно выбирает наиболее быстрый для себя маршрут движения.
Кто из них прибежит первым? км, разбитого на три полосы, шириной по 4 км. Одна из крайних полос покрыта снегом, другая — песком, а на средней полосе залит каток. Конькобежец бежит по льду со скоростью 12 км/ч, по снегу 4 км/ч, а по песку — 3 км/ч. Лыжник бежит по льду со скоростью 3 км/ч, по снегу
12 км/ч, а по песку — 4 км/ч. Атлет бежит по льду со скоростью 4 км/ч, по снегу 3 км/ч, а по песку — 12 км/ч. Все трое одновременно стартуют из
одного угла лугопарка, чтобы финишировать в противоположном. Каждый из
них самостоятельно выбирает наиболее быстрый для себя маршрут движения.
Кто из них прибежит первым?
Можно ли в квадрате 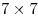 поместить 100 правильных треугольников со стороной 1? поместить 100 правильных треугольников со стороной 1?
Назовем почтипараллелограммом четырехугольник, направления противоположных сторон которого различаются меньше, чем на 1 градус. Окружность разбили на 2007 дуг, а точки деления соединили хордами. Можно ли утверждать, что среди них найдутся 4 хорды, точки пересечения которых лежат внутри круга и являются вершинами почтипараллелограмма?
Петя последовательно выписывает натуральные числа от 1 до n в системе счисления с основанием 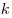 , ищет их общую сумму цифр , ищет их общую сумму цифр 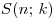 и проверяет, не окажется ли она равной 2007. Меняя и проверяет, не окажется ли она равной 2007. Меняя 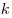 , из подходящих вариантов он оставляет только те, в которых , из подходящих вариантов он оставляет только те, в которых  окажется наименьшим возможным. При каких окажется наименьшим возможным. При каких 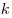 это случится? это случится?
Сколько целых корней имеет уравнение 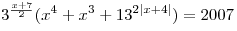 ? ?
Два игрока по очереди ставят цифры в свободные клетки квадрата 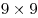 . Тот, кто ставит первую цифру, стремится сделать так, чтобы в каждой строчке, каждом столбце и каждом из 9 квадратов . Тот, кто ставит первую цифру, стремится сделать так, чтобы в каждой строчке, каждом столбце и каждом из 9 квадратов 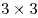 , на которые разбивается основной квадрат, все 9 цифр оказались различными. Второй старается помешать первому. Однако он не имеет права нарушать названные правила до тех пор, пока остается иная возможность. Кто из них достигнет своей цели, если будет действовать наилучшим образом? , на которые разбивается основной квадрат, все 9 цифр оказались различными. Второй старается помешать первому. Однако он не имеет права нарушать названные правила до тех пор, пока остается иная возможность. Кто из них достигнет своей цели, если будет действовать наилучшим образом?
Задачи для 11 класса
Лугопарк имеет форму квадрата 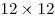 км, разбитого на три полосы, шириной по 4 км. Одна из крайних полос покрыта снегом, другая — песком, а на средней полосе залит каток. Конькобежец бежит по льду со скоростью 12 км/ч, по снегу 4 км/ч, а по песку — 3 км/ч. Лыжник бежит по льду со скоростью 3 км/ч, по снегу
12 км/ч, а по песку — 4 км/ч. Атлет бежит по льду со скоростью 4 км/ч, по снегу 3 км/ч, а по песку — 12 км/ч. Все трое одновременно стартуют из
одного угла лугопарка, чтобы финишировать в противоположном. Каждый из
них самостоятельно выбирает наиболее быстрый для себя маршрут движения.
Кто из них прибежит первым? км, разбитого на три полосы, шириной по 4 км. Одна из крайних полос покрыта снегом, другая — песком, а на средней полосе залит каток. Конькобежец бежит по льду со скоростью 12 км/ч, по снегу 4 км/ч, а по песку — 3 км/ч. Лыжник бежит по льду со скоростью 3 км/ч, по снегу
12 км/ч, а по песку — 4 км/ч. Атлет бежит по льду со скоростью 4 км/ч, по снегу 3 км/ч, а по песку — 12 км/ч. Все трое одновременно стартуют из
одного угла лугопарка, чтобы финишировать в противоположном. Каждый из
них самостоятельно выбирает наиболее быстрый для себя маршрут движения.
Кто из них прибежит первым?
Можно ли в квадрате 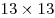 поместить 375 правильных треугольников со стороной 1? поместить 375 правильных треугольников со стороной 1?
Назовем почтипараллелограммом четырехугольник, направления противоположных сторон которого различаются меньше, чем на 1 градус. Окружность разбили на 2007 дуг, а точки деления соединили хордами. Можно ли утверждать, что среди них найдутся 4 хорды, точки пересечения которых лежат внутри круга и являются вершинами почтипараллелограмма?
Существует ли функция, значения которой и ее 2007 производных при 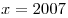 равны 2007? равны 2007?
Сферы радиусов 1, 2 и 3 попарно касаются друг друга. Найдите радиус круга, вписанного в треугольник, образованный их центрами.
Два игрока по очереди ставят цифры в свободные клетки квадрата 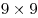 . Тот, кто ставит первую цифру, может ставить только нечетные цифры. Он стремится сделать так, чтобы в каждой строчке, каждом столбце и каждом из 9 квадратов . Тот, кто ставит первую цифру, может ставить только нечетные цифры. Он стремится сделать так, чтобы в каждой строчке, каждом столбце и каждом из 9 квадратов 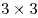 , на которые разбивается основной квадрат, все 9 цифр оказались различными. Второй может ставить только четные цифры и старается помешать первому. Однако он не имеет права нарушать названные правила до тех пор, пока остается иная возможность. Кто из них достигнет своей цели, если будет действовать наилучшим образом? , на которые разбивается основной квадрат, все 9 цифр оказались различными. Второй может ставить только четные цифры и старается помешать первому. Однако он не имеет права нарушать названные правила до тех пор, пока остается иная возможность. Кто из них достигнет своей цели, если будет действовать наилучшим образом?
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
|

