МЕЖДУНАРОДНАЯ ДИСТАНЦИОННАЯ МАТЕМАТИЧЕСКАЯ ОЛИМПИАДА «ТРЕТЬЕ ТЫСЯЧЕЛЕТИЕ»
2005 год

Задачи для 5 класса

1. В театре есть три прожектора — красный, синий и желтый, которыми с помощью переключателей управляют два осветителя. Переключатель позволяет зажечь любой погашенный прожектор, либо погасить зажженный. Комбинация красного и синего цветов дает фиолетовый, красного и желтого — оранжевый, а синего и желтого — зеленый. Включение сразу всех прожекторов назовем белым цветом, а гашение всех — черным. В некоторый момент сцена была окрашена в оранжевый цвет. Что произойдет, если одновременно, но не сговариваясь друг с другом, один из осветителей захочет перекрасить ее в фиолетовый цвет, а другой — в зеленый?

2. Министр финансов Дурляндии выпустил в обращение только монеты достоинством в 7 и 11 дуриков. Покупатель должен заплатить продавцу ровно 5 дуриков. Сумеют ли они рассчитаться, если у каждого из них есть только по 4 монеты того и другого достоинства?

3. Какой день недели наступит ровно через 2005 недель после 24 января 2005 года?

4. Квадратную клеточку можно двумя способами разбить диагональю на два треугольника. Если один из треугольников закрасить, то такую фигуру назовем ежиком. Двух ежиков нельзя размещать на клетчатой бумаге так, чтобы они имели общую сторону. Какое наименьшее число ежиков и как можно расположить в квадрате 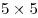клеток, чтобы к ним с соблюдением данного условия уже нельзя было добавить ни одного нового?

5. Слиток имеет форму кирпича и весит 10 килограмм. Его муляж на 20% короче, на 25% шире и сделан из вдвое более легкого материала. Оказалось, что весят они одинаково. Что выше — муляж или слиток — и на сколько процентов?

6. Существует ли натуральное число, сумма цифр которого больше его самого?

Задачи для 6 класса

1. Назовите дату, ровно на 2005 недель более раннюю, чем 24 января 2005 года.

2. В театре есть три прожектора — красный, синий и желтый, которыми с помощью переключателей управляют два осветителя. Переключатель позволяет зажечь любой погашенный прожектор, либо погасить зажженный. Комбинация красного и синего цветов дает фиолетовый, красного и желтого — оранжевый, а синего и желтого — зеленый. Включение сразу всех прожекторов назовем белым цветом, а гашение всех — черным. В некоторый момент сцена была окрашена в оранжевый цвет. Что произойдет, если одновременно, но не сговариваясь друг с другом, один из осветителей захочет перекрасить ее в фиолетовый цвет, а другой — в зеленый?

3. Министр финансов Дурляндии выпустил в обращение только монеты достоинством в 7 и 11 дуриков. Покупатель должен заплатить продавцу ровно 5 дуриков. Сумеют ли они рассчитаться, если у каждого из них есть только по 3 монеты того и другого достоинства?

4. Слиток имеет форму кирпича и весит 10 килограмм. Его муляж на 60% короче, на 25% уже и сделан из вдвое более легкого материала. Оказалось, что весят они одинаково. Что выше — муляж или слиток — и на сколько процентов?

5. Квадратную клеточку можно двумя способами разбить диагональю на два треугольника. Если один из треугольников закрасить, то такую фигуру назовем ежиком. Двух ежиков нельзя размещать на клетчатой бумаге так, чтобы они имели общую сторону. Какое наименьшее число ежиков и как можно расположить в квадрате 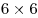клеток, чтобы к ним с соблюдением данного условия уже нельзя было добавить ни одного нового?

6. Если одно число с суммой цифр, делящейся на 3, умножить на другое число с таким же свойством, то всегда получится число с суммой цифр, делящейся на 9. Сохранится ли истинность этого утверждения, если 3 и 9 заменить в нем на 333 и 999?

Задачи для 7 класса

1. Можно ли получить ромб, приложив друг к другу несколько копий одного и того же разностороннего треугольника?

2. Назовите дату, ровно на 2005 недель более позднюю, чем 24 января 2005 года.

3. Можно ли так расставить на шахматной (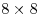) доске цифры от 0 до 9, чтобы в клетках, соседних с каждой (их от 3 до 8), стояли только различные цифры, и ни для каких двух клеток не повторялась бы очередность этих соседних номеров при обходе вокруг клетки против часовой стрелки.

4. Алекс написал на карточках числа от 10000 до 99999. Затем он выбрал из них десять неизвестно каких карточек и хочет выложить их друг за другом так, чтобы полученное 50-значное число не делилось на 41. Всегда ли он сможет так сделать?

5. В театре есть три прожектора — красный, синий и желтый, которыми с помощью переключателей управляют два осветителя. Переключатель позволяет зажечь любой погашенный прожектор, либо погасить зажженный. Комбинация красного и синего цветов дает фиолетовый, красного и желтого — оранжевый, а синего и желтого — зеленый. Включение сразу всех прожекторов назовем белым цветом, а гашение всех — черным. Окончательно запутавшись, осветители хотят занумеровать эти восемь цветов числами и придумать такую операцию над номерами, чтобы ее выполнение позволяло быстро и легко определить, как именно заменить любой из цветов любым другим. Помогите им решить эту проблему.

6. Министр финансов Дурляндии выпустил в обращение только монеты достоинством в 7 и 11 дуриков. Покупатель должен заплатить продавцу ровно 5 дуриков. Сумеют ли они рассчитаться, если у каждого из них есть только по 3 монеты того и другого достоинства?

Задачи для 8 класса

1. Множество состоит из натуральных чисел, ни сумма, ни разность никаких двух из которых не делятся на 2005. Каково максимально возможное число элементов такого множества ?

2. Найдите наименьшее натуральное число, которое в трех системах счисления записывается (разными) парами одинаковых цифр.

3. Ник сумел сложить ромб из нескольких копий одного и того же разностороннего треугольника. Какое наименьшее число копий он мог для этого использовать?

4. Назовите уже прошедшую дату (год, месяц, число), которую от 24 января 2005 года отделяют ровно 32 года, 32 месяца, 32 недели и 32 дня.

5. Можно ли так расставить на шахматной (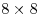) доске цифры от 0 до 9, чтобы в клетках, соседних с каждой (их от 3 до 8), стояли только различные цифры, и ни для каких двух клеток не повторялась бы очередность этих соседних номеров при обходе вокруг клетки против часовой стрелки.

6. Алекс написал на карточках числа от 0 до 99999. Затем на карточках, отвечающих числам, меньшим 10000, он приписал впереди столько нулей, чтобы на каждой карточке оказалось ровно 5 цифр. Он хочет выложить эти карточки друг за другом так, чтобы полученное 500000-значное число делилось на 41. Сможет ли он так сделать?

Задачи для 9 класса

1. Множество состоит из натуральных чисел, ни сумма, ни разность никаких двух из которых не делятся на 2005. Каково максимально возможное число элементов такого множества ?

2. Найдите наименьшее натуральное число, запись которого в трех разных системах счисления содержит ровно две единицы и несколько нулей (не менее одного).

3. На плоскости выбраны три точки. Постройте три попарно касающиеся окружности с центрами в этих точках.

4. Назовем средним антигеометрическим двух чисел квадратный корень из их неполного квадрата разности. Докажите, что среднее арифметическое положительных чисел всегда лежит между средним геометрическим и средним антигеометрическим этих же чисел.

5. Ник сумел сложить квадрат из нескольких копий одного и того же разностороннего треугольника. Какое наименьшее число копий он мог для этого использовать?

6. Назовите уже прошедшую дату (год, месяц, число), которую от 24 января 2005 года отделяют ровно 31 год, 31 месяц, 31 неделя и 31 день.

Задачи для 10 класса

1. Найдите наименьшее натуральное число, запись которого в трех разных системах счисления содержит ровно две единицы и несколько нулей (возможно, ни одного).

2. На плоскости выбраны три точки, не лежащие на одной прямой. Всегда ли и сколькими способами можно построить три попарно касающиеся окружности с центрами в этих точках?

3. Каждую вершину выпуклого пятиугольника соединили отрезком с точкой пересечения диагоналей четырехугольника, образованного оставшимися вершинами. Можно ли утверждать, что пять проведенных отрезков всегда пересекутся в одной точке?

4. Дан правильный тетраэдр (треугольная пирамида, все 6 ребер которой равны друг другу), Разрешается от одной из вершин «отпилить» кусок в форме треугольной пирамиды (не обязательно правильной). Может ли сумма длин всех ребер уменьшиться в результате этого действия?

5. Назовем средним антигеометрическим двух чисел квадратный корень из их неполного квадрата разности. Докажите, что среднее антигеометрическое не может быть меньше арифметического этих же чисел.

6. Назовите уже прошедшую дату (год, месяц, число), которую от 24 января 2005 года отделяют ровно 30 лет, 30 месяцев, 30 недель и 30 дней.

Задачи для 11 класса

1. Может ли производная произведения двух непостоянных функций равняться произведению их производных?

2. Четыре сферы попарно касаются друг друга. Могут ли их радиусы выражаться последовательными натуральными числами?

3. На плоскости выбраны три точки, не лежащие на одной прямой. Всегда ли и сколькими способами можно построить три попарно касающиеся окружности с центрами в этих точках?

4. Дан правильный тетраэдр (треугольная пирамида, все 6 ребер которой равны друг другу), Разрешается от одной из вершин «отпилить» кусок в форме треугольной пирамиды (не обязательно правильной). Может ли сумма длин всех ребер увеличиться в результате этого действия?

5. Назовите уже прошедшую дату (год, месяц, число), которую от 24 января 2005 года отделяют ровно 31 год, 30 месяцев, 29 недель и 28 дней.

6. Алекс написал на карточках числа от 0 до 99999. Затем на карточках, отвечающих числам, меньшим 10000, он приписал впереди столько нулей, чтобы на каждой карточке оказалось ровно 5 цифр. Он хочет выложить эти карточки друг за другом так, чтобы полученное 500000-значное число не делилось на 41. Сможет ли он так сделать?

Задачи для 12 класса

1. Может ли квадрат производной непостоянной функции равняться производной от ее квадрата?

2. Множество состоит из натуральных чисел. Ни для какого его подмножества сумма элементов не делится на 2005. Каково максимально возможное число элементов такого множества ?

3. Найдите наименьшее натуральное число, которое в четырех системах счисления записывается (разными) парами одинаковых цифр.

4. Четыре сферы попарно касаются друг друга. Могут ли их радиусы выражаться натуральными числами?

5. Петр хочет построить такой чертеж из нескольких окружностей на плоскости, чтобы каждые две из них имели ровно одну общую точку, но при этом никакая точка не была бы общей сразу для трех окружностей. Каково максимально возможное число окружностей на таком чертеже?

6. Назовите уже прошедшую дату (год, месяц, число), которую от 24 января 2005 года отделяют ровно 31 год, 29 месяцев, 27 недель и 25 дней.