|
МЕЖДУНАРОДНАЯ ДИСТАНЦИОННАЯ МАТЕМАТИЧЕСКАЯ ОЛИМПИАДА «ТРЕТЬЕ ТЫСЯЧЕЛЕТИЕ»
2004 год
Задачи для 5 класса
Известно, что в пьяном виде маляр работает вдвое медленнее, чем в трезвом. В первую неделю он покрасил на 300 метров забора больше, чем во вторую, потому что во вторую неделю пьянствовал на два дня больше, чем в первую. Сколько метров забора в день красит трезвый маляр?
Санкт-Петербург основан в 1703 году. Наступит ли когда-нибудь такой год, в котором Санкт-Петербургу исполнится столько лет, сколько получится, если откинуть от этого года первую цифру?
Один гость, приезжавший на юбилей Санкт-Петербурга, тратил деньги только на поездки в метро (по 7 рублей за жетон) и походы в музеи (по 50 рублей за визит). Позже он подсчитал свои расходы и только по ним понял, сколько раз он ездил на метро и сколько раз ходил в музей. Какой суммы не могли в этом случае превысить его расходы?
Вы видите, как на стенке то появляются, то исчезают светящиеся трехзначные числа. На стене написано, что каждое следующее число — это три последние цифры произведения двух предыдущих чисел. Вспыхивает число 995, после этого — еще несколько чисел, которых Вы не запомнили, затем появляется 998. Можно ли верить надписям на стенах?
Найдите количество таких трехзначных чисел, у которых все цифры различны, первая цифра делится на 3, вторая — на 2.
Лев придумал новую алгебру, в которой сумма чисел  и и  выражается через обычные арифметические действия формулой выражается через обычные арифметические действия формулой  . Чему в новой алгебре Льва равно произведение 2 на 2? . Чему в новой алгебре Льва равно произведение 2 на 2?
Задачи для 6 класса
Москва основана в 1147 году. Был ли и будет ли когда-нибудь такой год, в котором Москве исполняется столько лет, сколько получится, если откинуть от этого года первую цифру?
Лев придумал новую алгебру, в которой сумма чисел  и и  выражается через обычные арифметические действия формулой выражается через обычные арифметические действия формулой  . Чему в новой алгебре Льва равно произведение 3 на 3? . Чему в новой алгебре Льва равно произведение 3 на 3?
На клетчатой бумаге по линиям прямоугольной сетки со стороной 1 построена замкнутая ломаная длины 24. Какую наибольшую площадь может охватить эта ломаная?
Найдите количество таких трехзначных чисел, у которых все цифры различны, первая цифра делится на 3, вторая — на 2.
Найдите наименьшее натуральное число, которое нацело делится на 2000, 2001, 2002, 2003 и 2004.
Лев купил себе на завтрак стакан сока, салат и кусочек хлеба. Он заметил, что цена сока составляет столько же процентов от цены всего завтрака, сколько цена салата от цены сока. А выпив сок, он понял, что цена хлеба составляет 10% от цены оставшейся части завтрака. Сколько процентов от цены завтрака составляла цена салата?
Задачи для 7 класса
Три года назад внучка была втрое младше деда, а через 16 лет будет вдвое младше. Сколько лет каждому?
Известно, что в пьяном виде маляр работает вдвое медленнее, чем в трезвом. В первую неделю он покрасил на 300 метров забора больше, чем во вторую, потому что во вторую неделю пьянствовал на два дня больше, чем в первую. Сколько метров забора в день красит трезвый маляр?
Лев придумал новую алгебру, в которой сумма чисел  и и  выражается через обычные арифметические действия формулой выражается через обычные арифметические действия формулой  . Равны ли в новой алгебре Льва произведения 3 на 4 и 4 на 3? . Равны ли в новой алгебре Льва произведения 3 на 4 и 4 на 3?
На плоскости провели 4 прямых, в результате чего она разбилась на несколько областей. В каждую область записали число участков, из которых состоит ее граница (эти участки могут быть отрезками, лучами или целыми прямыми). Найдите наибольшее и наименьшее значения суммы всех записанных чисел.
Найдите наименьшее натуральное число, которое нацело делится на 2000, 2001, 2002, 2003 и 2004.
Перед Вами оказывается шесть дверей, и к каждой прикреплена табличка. Из надписей на стенах Вы узнаете, что за одной дверью — выход, за остальными — либо ложные ходы, либо свирепые людоеды. Если за дверью выход, то на табличке, прикрепленной к этой двери, написана правда, если людоед — ложь, а на дверях с ложными ходами может быть написано все, что угодно. Ошибаться не стоит: о свирепости людоедов красноречиво свидетельствуют обглоданные человеческие кости, беспорядочно разбросанные по всему помещению. В какую дверь Вам следует войти?
| За этой дверью нет выхода |
|
|
|
|
| За этой дверью то же, что и за дверью 6 |
|
| На дверях 1 и 6 написаны утверждения одинаковой истинности |
|
|
| За дверью 2 — очень голодный людоед |
|
|
|
Задачи для 8 класса
Один гость, приезжавший на юбилей Санкт-Петербурга, тратил деньги только на поездки в метро (по 7 рублей за жетон) и походы в музеи (по 50 рублей за визит). Позже он подсчитал свои расходы и только по ним понял, сколько раз он ездил на метро и сколько раз ходил в музей. Какой суммы не могли в этом случае превысить его расходы?
На плоскости построены несколько окружностей, никакие две из которых не пересекаются (но какие-то могут лежать внутри других). Назовем две окружности соседними, если на каждой из них можно выбрать по точке, отрезок между которыми не имеет общих точек ни с одной из остальных окружностей. Для каждой из построенных окружностей сосчитали число соседних с ней. Могла ли сумма всех этих чисел оказаться равной 2004?
Лев придумал новую алгебру, в которой сумма чисел  и и  выражается через обычные арифметические действия формулой выражается через обычные арифметические действия формулой  . Чему в новой алгебре Льва равно произведение 8 на 8? . Чему в новой алгебре Льва равно произведение 8 на 8?
Дед Мороз увидел 2004 детей, выстроившихся по кругу. Проблема выдачи подарков заключалась в том, что двоечникам полагается один подарок, а всем остальным — два. Кроме того, двоечники вечно говорят неправду, в то время как остальные дети правдивы. Дед Мороз спросил: «Сколько подарков нужно давать стоящему слева от вас?», после чего сложил ответы детей. Потом он спросил: «Сколько подарков нужно давать стоящему справа от вас?», после чего сложил эти ответы. Как сильно могут отличаться эти две суммы друг от друга?
На клетчатой бумаге по линиям прямоугольной сетки со стороной 1 построена замкнутая ломаная длины 2004. Какую наибольшую площадь может охватить эта ломаная?
Перед Вами оказывается шесть дверей, и к каждой прикреплена табличка. Из надписей на стенах Вы узнаете, что за одной дверью — выход, за остальными — либо ложные ходы, либо свирепые людоеды. Если за дверью выход, то на табличке, прикрепленной к этой двери, написана правда, если людоед — ложь, а на дверях с ложными ходами может быть написано все, что угодно. Ошибаться не стоит: о свирепости людоедов красноречиво свидетельствуют обглоданные человеческие кости, беспорядочно разбросанные по всему помещению. В какую дверь Вам следует войти?
| За этой дверью нет выхода |
|
|
|
|
| За этой дверью то же, что и за дверью 6 |
|
| На дверях 1 и 6 написаны утверждения одинаковой истинности |
|
|
| За дверью 2 — очень голодный людоед |
|
|
|
Задачи для 9 класса
Вы видите, как на стенке то появляются, то исчезают светящиеся трехзначные числа. На стене написано, что каждое следующее число — это три последние цифры произведения двух предыдущих чисел. Вспыхивает число 995, после этого — еще несколько чисел, которых Вы не запомнили, затем появляется 998. Можно ли верить надписям на стенах?
Лев построил ломаную  , все звенья которой равны 1, причем каждое звено , все звенья которой равны 1, причем каждое звено  перпендикулярно соответствующему радиусу перпендикулярно соответствующему радиусу  . Найдите длину последнего радиуса . Найдите длину последнего радиуса  . .
Известно, что уравнение  имеет 3 различных положительных корня. Докажите, что произведение коэффициентов имеет 3 различных положительных корня. Докажите, что произведение коэффициентов  и и 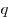 этого уравнения не может быть меньше 9. этого уравнения не может быть меньше 9.
На плоскости построены несколько окружностей, никакие две из которых не пересекаются (но какие-то могут лежать внутри других). Назовем две окружности соседними, если на каждой из них можно выбрать по точке, отрезок между которыми не имеет общих точек ни с одной из остальных окружностей. Для каждой из построенных окружностей сосчитали число соседних с ней. Могла ли сумма всех этих чисел оказаться равной 2004?
Лев придумал новую алгебру, в которой сумма чисел  и и  выражается через обычные арифметические действия формулой выражается через обычные арифметические действия формулой  . Чему в новой алгебре Льва равно 2 во второй степени? . Чему в новой алгебре Льва равно 2 во второй степени?
Существует ли треугольник, длины всех сторон которого — целые числа, одна из них равна 2004, но площадь треугольника меньше 1?
Задачи для 10 класса
Лев придумал новую алгебру, в которой сумма чисел  и и  выражается через обычные арифметические действия формулой выражается через обычные арифметические действия формулой  . Чему в новой алгебре Льва равно 2 в третьей степени? . Чему в новой алгебре Льва равно 2 в третьей степени?
Существует ли треугольник, длины всех сторон которого — целые числа, одна из них равна 2004, но площадь треугольника меньше 1000?
Известно, что уравнение  имеет 3 различных положительных корня. Докажите, что произведение коэффициентов имеет 3 различных положительных корня. Докажите, что произведение коэффициентов  и и 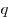 этого уравнения не может быть меньше 9. этого уравнения не может быть меньше 9.
На плоскости провели несколько прямых, в результате чего она разбилась на многоугольные области. Вершинами этих областей являются точки пересечения проведенных прямых, а сторонами — отрезки (между вершинами), лучи (выходящие из вершин), либо (в исключительных случаях) целые прямые. В каждую область записали число ограничивающих ее сторон. Оказалось, что сумма записанных чисел равна 2004. Каким в этом случае могло быть число прямых?
Найдите все пары натуральных чисел  и и  , для которых справедливо равенство , для которых справедливо равенство  . .
Для каждого натурального 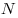 через через  обозначим число целочисленных решений уравнения обозначим число целочисленных решений уравнения  . Сколько цифр имеет десятичная запись числа . Сколько цифр имеет десятичная запись числа  ? ?
Задачи для 11 класса
Обозначим через  произведение двучленов произведение двучленов  , ,  , ,  , ,  . Найдите все такие . Найдите все такие  , при которых уравнение , при которых уравнение  имеет целый корень. имеет целый корень.
Известно, что углы  и и  — острые и удовлетворяют двум уравнениям: — острые и удовлетворяют двум уравнениям:  и и  . Выразите угол . Выразите угол  в градусах. в градусах.
Правильным тетраэдром называется треугольная пирамида, все 6 ребер которой равны друг другу. Пусть точка 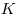 — середина ребра — середина ребра 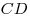 правильного тетраэдра правильного тетраэдра 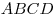 . В плоскости . В плоскости  построена окружность, касающаяся луча построена окружность, касающаяся луча  в точке в точке  , а луча , а луча  в точке в точке  . Через . Через 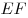 обозначен параллельный обозначен параллельный  диаметр этой окружности. Найдите величину угла диаметр этой окружности. Найдите величину угла  . .
Для каждого натурального 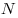 через через  обозначим число целочисленных решений уравнения обозначим число целочисленных решений уравнения  . Сколько цифр имеет десятичная запись числа . Сколько цифр имеет десятичная запись числа  ? ?
Лев придумал новую алгебру, в которой сумма чисел  и и  выражается через обычные арифметические действия формулой выражается через обычные арифметические действия формулой  . Существуют ли в новой алгебре Льва такие различные положительные числа . Существуют ли в новой алгебре Льва такие различные положительные числа 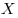 и и 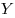 , для которых равны произведения , для которых равны произведения 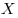 на на 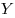 и и 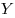 на на 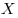 ? ?
Докажите для 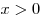 неравенство неравенство  . .
Задачи для 12 класса
Что на самом деле обозначено буквой 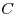 в известной формуле в известной формуле  ? ?
Лев построил ломаную  , все звенья которой равны 1, причем каждое звено , все звенья которой равны 1, причем каждое звено  перпендикулярно соответствующему радиусу перпендикулярно соответствующему радиусу  . Найдите длину последнего радиуса . Найдите длину последнего радиуса  . .
Опишите множество всех таких функций 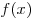 , для которых при любом вещественном , для которых при любом вещественном  выполняется равенство выполняется равенство  . .
Правильным тетраэдром называется треугольная пирамида, все 6 ребер которой равны друг другу. Пусть точка 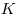 — середина ребра — середина ребра 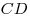 правильного тетраэдра правильного тетраэдра 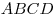 . В плоскости . В плоскости  построена окружность, касающаяся луча построена окружность, касающаяся луча  в точке в точке  , а луча , а луча  в точке в точке  . Через . Через 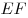 обозначен параллельный обозначен параллельный  диаметр этой окружности. Найдите величину угла диаметр этой окружности. Найдите величину угла  . .
Для каждого натурального 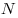 через через  обозначим число целочисленных решений уравнения обозначим число целочисленных решений уравнения  . Сколько цифр имеет десятичная запись числа . Сколько цифр имеет десятичная запись числа  ? ?
Магазин продает компьютер в кредит на следующих условиях. В день покупки покупатель платит 1800 рублей, которые составляют 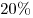 от полной цены. Затем в последний день каждого из 12 последующих месяцев (начиная со дня покупки) он платит по 777 рублей. С точностью до от полной цены. Затем в последний день каждого из 12 последующих месяцев (начиная со дня покупки) он платит по 777 рублей. С точностью до  найдите, под какой среднегодовой процент магазин кредитует таких покупателей. найдите, под какой среднегодовой процент магазин кредитует таких покупателей.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
|

