|
МЕЖДУНАРОДНАЯ ДИСТАНЦИОННАЯ МАТЕМАТИЧЕСКАЯ ОЛИМПИАДА «ТРЕТЬЕ ТЫСЯЧЕЛЕТИЕ»
2003 год
Задачи для 5 класса
В одной из 16 клеток доски 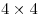 стоит Шуршавчик, который может ходить по горизонтали или по вертикали на 2 или на 3 клетки (перелетая по воздуху через 1 или 2 клетки). Выберите одну из клеток доски и, начав с нее, обойдите Шуршавчиком как можно больше клеток, не вставая ни на какую более одного раза. Порядок обхода клеток укажите номерами 1, 2, 3, ... стоит Шуршавчик, который может ходить по горизонтали или по вертикали на 2 или на 3 клетки (перелетая по воздуху через 1 или 2 клетки). Выберите одну из клеток доски и, начав с нее, обойдите Шуршавчиком как можно больше клеток, не вставая ни на какую более одного раза. Порядок обхода клеток укажите номерами 1, 2, 3, ...
Из пяти различных цифр Миша составил пятизначное число. Взяв оставшиеся пять цифр, Леша тоже составил из них пятизначное число. Наташа сложила числа мальчиков. Могло ли у нее получиться число, в котором три единицы и три двойки?
Жулик попросил у продавщицы Маши бутылку лимонада за 30 рублей, дав фальшивую 100-рублевую купюру. Сдачи у Маши не было, и она разменяла купюру в соседнем ларьке у продавца Васи. Когда жулик ушел, Вася понял, что купюра фальшивая, и Маше пришлось отдать ему настоящие 100 рублей. Какой убыток понесла Маша?
Аня умножила номер своей квартиры не то на 6, не то на 7. Боря прибавил к результату Ани не то 6, не то 7. Ваня отнял от результата Бори не то 6, не то 7. В итоге получилось 2003. Какой номер у Аниной квартиры?
Кот Леопольд хочет подарить 9 мышатам одну коробку конфет, в которой должно быть столько конфет, чтобы мышата смогли поделить их, не ломая, так, чтобы каждому досталась хотя бы одна конфета и никто из мышат не получил конфет поровну. В магазине продаются коробки, в которых конфет 40, 45, 50 и 55. Какие из них не стоит покупать коту Леопольду?
Если последние три цифры числа 2003 записать в обратном порядке, то получится 300. Именно 300 лет исполняется Санкт-Петербургу в мае 2003 года. Как скоро наступит следующий год с таким же свойством?
Задачи для 6 класса
В одной из 16 клеток доски 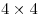 стоит Шуршавчик, который может ходить по горизонтали или по вертикали на 2 или на 3 клетки (перелетая по воздуху через 1 или 2 клетки). Выберите одну из клеток поля и, начав с нее, обойдите Шуршавчиком как можно больше клеток, не вставая ни на какую более одного раза. Порядок обхода клеток укажите номерами 1 ,2, 3, ... стоит Шуршавчик, который может ходить по горизонтали или по вертикали на 2 или на 3 клетки (перелетая по воздуху через 1 или 2 клетки). Выберите одну из клеток поля и, начав с нее, обойдите Шуршавчиком как можно больше клеток, не вставая ни на какую более одного раза. Порядок обхода клеток укажите номерами 1 ,2, 3, ...
Из пяти различных цифр Дима составил пятизначное число. Взяв оставшиеся пять цифр, Влад тоже составил из них пятизначное число. Георгий сложил числа мальчиков. Могло ли у него получиться число, в котором только единицы и двойки?
В последовательности 1, 1, 2, 3, 5, 8, 13, ... каждое число, начиная с третьего, равно сумме двух предыдущих. Могут ли в этой последовательности встретиться подряд два числа, кратных 2003?
Предприимчивый Георгий купил на рынке партию ручек и предлагает одноклассникам либо одну ручку за 5 рублей, либо три ручки за 10 рублей, потому что хочет от каждого покупателя получить одинаковую прибыль. А за сколько рублей Георгию в таком случае надо продавать ручки покупателю, который хочет купить 5 ручек?
Катя Угольникова нарисовала несколько углов, величина каждого из которых больше 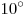 , меньше , меньше 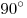 и выражается целым числом градусов. При каком наименьшем количестве нарисованных углов можно утверждать, что среди них есть хотя бы три равных? и выражается целым числом градусов. При каком наименьшем количестве нарисованных углов можно утверждать, что среди них есть хотя бы три равных?
Если последние три цифры числа 2003 записать в обратном порядке, то получится 300. Именно 300 лет исполняется Санкт-Петербургу в мае 2003 года. Сколько еще раз в XXI веке наступит год с таким же свойством?
Задачи для 7 класса
В одной из 16 клеток доски 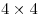 стоит Шуршавчик, который может ходить по горизонтали или по вертикали на 2 или на 3 клетки (перелетая по воздуху через 1 или 2 клетки). Выберите одну из клеток поля и, начав с нее, обойдите Шуршавчиком как можно больше клеток, не вставая ни на какую более одного раза. Порядок обхода клеток укажите номерами 1, 2, 3, ... стоит Шуршавчик, который может ходить по горизонтали или по вертикали на 2 или на 3 клетки (перелетая по воздуху через 1 или 2 клетки). Выберите одну из клеток поля и, начав с нее, обойдите Шуршавчиком как можно больше клеток, не вставая ни на какую более одного раза. Порядок обхода клеток укажите номерами 1, 2, 3, ...
Из пяти различных цифр Костя составил пятизначное число. Взяв оставшиеся пять цифр, Дима тоже составил из них пятизначное число. Маша сложила числа мальчиков. Могло ли у нее получиться число, в котором только две различных цифры, причем у них поровну повторов?
Светлана Сергеевна дала ученикам задание: сократить дробь 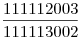 . Через некоторое время старательная Наташа сказала, что сократила дробь, а ленивый Андрей говорит, что дробь несократима. Кто из них прав? . Через некоторое время старательная Наташа сказала, что сократила дробь, а ленивый Андрей говорит, что дробь несократима. Кто из них прав?
Можно ли из каких-нибудь двух различных равнобедренных треугольников сложить прямоугольный треугольник, у которого один из острых углов на 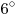 больше другого? больше другого?
Клетки доски 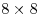 , которые сначала все были белого цвета, по очереди закрашивают в синий цвет так, чтобы после закрашивания каждой клетки фигура, состоящая из синих клеток, имела ось симметрии. Соблюдая это условие, закрасьте как можно больше клеток (доказательства максимальности не требуется). Порядок закраски клеток укажите номерами 1, 2, 3, ... , которые сначала все были белого цвета, по очереди закрашивают в синий цвет так, чтобы после закрашивания каждой клетки фигура, состоящая из синих клеток, имела ось симметрии. Соблюдая это условие, закрасьте как можно больше клеток (доказательства максимальности не требуется). Порядок закраски клеток укажите номерами 1, 2, 3, ...
Если последние три цифры числа 2003 записать в обратном порядке, то получится 300. Именно 300 лет исполняется Санкт-Петербургу в мае 2003 года. Случались ли прежде в истории Санкт-Петербурга годы с таким же свойством?
Задачи для 8 класса
В одной из 16 клеток доски 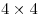 стоит Шуршавчик, который может ходить по горизонтали или по вертикали на 2 или на 3 клетки (перелетая по воздуху через 1 или 2 клетки). Выберите одну из клеток поля и, начав с нее, обойдите Шуршавчиком как можно больше клеток, не вставая ни на какую более одного раза. Порядок обхода клеток укажите номерами 1, 2, 3, ... стоит Шуршавчик, который может ходить по горизонтали или по вертикали на 2 или на 3 клетки (перелетая по воздуху через 1 или 2 клетки). Выберите одну из клеток поля и, начав с нее, обойдите Шуршавчиком как можно больше клеток, не вставая ни на какую более одного раза. Порядок обхода клеток укажите номерами 1, 2, 3, ...
Внутри квадрата 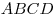 взята такая точка взята такая точка 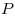 , что , что 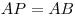 . Прямая . Прямая 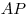 пересекает отрезок пересекает отрезок  в точке в точке 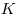 . Прямая . Прямая 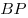 пересекает отрезок пересекает отрезок 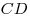 в точке в точке 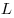 . Докажите, что . Докажите, что 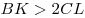 . .
В олимпиаде участвовали 13 мальчиков и 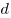 девочек. Все вместе они набрали девочек. Все вместе они набрали 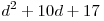 баллов, причем все набрали по одинаковому целому числу баллов. Сколько всего было участников олимпиады? баллов, причем все набрали по одинаковому целому числу баллов. Сколько всего было участников олимпиады?
Могут ли три человека, имея один двухместный велосипед, преодолеть расстояние 21 км за 3 часа, если скорость пешехода 5, велосипедиста с пассажиром — 10, а велосипедиста без пассажира — 15?
Петя написал несколько многочленов, возвел каждый в квадрат и сложил результаты. Могло ли у него в итоге получиться выражение 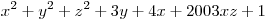 ? ?
Если последние три цифры числа 2003 записать в обратном порядке, то получится 300. Именно 300 лет исполняется Санкт-Петербургу в мае 2003 года. Сколько раз за следующие 300 лет истории города наступит год с таким же свойством?
Задачи для 9 класса
На стороне 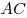 треугольника треугольника  взяты точки взяты точки 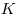 и и 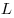 такие, что такие, что 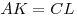 , а на сторонах , а на сторонах  и и  — точки — точки  и и 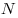 такие, что такие, что 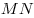 и и 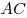 параллельны. Докажите, что точка параллельны. Докажите, что точка 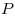 пересечения прямых пересечения прямых 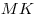 и и 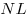 лежит на медиане треугольника лежит на медиане треугольника  или на ее продолжении. или на ее продолжении.
Можно ли расставить в квадрате 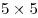 числа от 1 до 25 так, чтобы сумма чисел в каждой строке и в каждом столбце была бы простым числом? числа от 1 до 25 так, чтобы сумма чисел в каждой строке и в каждом столбце была бы простым числом?
На кольцевом троллейбусном маршруте движение начинается в 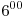 и заканчивается в и заканчивается в 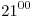 . В норме машины следуют с равными интервалами по 15 минут и проходят кольцо ровно за 1 час. Однажды из-за ремонта на одной из улиц образовалась пробка, на прохождение которой троллейбусы тратили по 25 минут вместо обычных 5 минут. Каким оказался средний интервал движения на маршруте в этот день? . В норме машины следуют с равными интервалами по 15 минут и проходят кольцо ровно за 1 час. Однажды из-за ремонта на одной из улиц образовалась пробка, на прохождение которой троллейбусы тратили по 25 минут вместо обычных 5 минут. Каким оказался средний интервал движения на маршруте в этот день?
Произведение двух составных чисел оказалось ровно на 2003 больше их суммы. Найдите эти числа.
Четыре точки плоскости попарно соединили друг с другом. Какое наибольшее число из всех образованных ими углов могут оказаться равными друг другу?
Если последние три цифры числа 2003 записать в обратном порядке, то получится 300. Именно 300 лет исполняется Санкт-Петербургу в мае 2003 года. В каком из веков истории Санкт-Петербурга дат с таким свойством больше: в одном из трех прошедших или в наступающем?
Задачи для 10 класса
Какое наибольшее число точек можно расположить на данной окружности так, чтобы во всех образованных ими треугольниках ни один из углов не был меньше 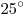 ? ?
Можно ли числа от 1 до 100 так расставить в квадрате 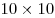 , чтобы сумма чисел в каждой строке и в каждом столбце была бы простым числом? , чтобы сумма чисел в каждой строке и в каждом столбце была бы простым числом?
Если последние три цифры числа 2003 записать в обратном порядке, то получится 300. Именно 300 лет исполняется Санкт-Петербургу в мае 2003 года. В каком из веков в III тысячелетии больше всего лет с таким же свойством?
На стороне 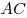 треугольника треугольника  взяты точки взяты точки 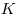 и и 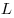 такие, что такие, что 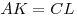 , а на сторонах , а на сторонах  и и  — точки — точки  и и 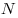 такие, что такие, что 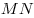 и и 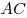 параллельны. Докажите, что точка параллельны. Докажите, что точка 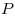 пересечения прямых пересечения прямых 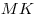 и и 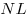 лежит на медиане треугольника лежит на медиане треугольника  или на ее продолжении. или на ее продолжении.
Представьте число 2003 в виде суммы кубов натуральных чисел, взяв для этого как можно меньшее число слагаемых.
Если на плоском листе провести 4 прямые общего положения, то на получившемся чертеже можно найти 4 различных треугольника. Какое наименьшее число прямых нужно провести, чтобы на получившемся чертеже можно было найти 2003 различных треугольника?
Задачи для 11-12 классов
Если последние три цифры числа 2003 записать в обратном порядке, то получится 300. Именно 300 лет исполняется Санкт-Петербургу в мае 2003 года. Сколько еще раз в III тысячелетии наступит год с таким же свойством?
На продолжении стороны  прямоугольника прямоугольника 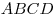 отложен отрезок отложен отрезок 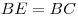 . Докажите, что проходящий через точку . Докажите, что проходящий через точку 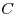 перпендикуляр к прямой перпендикуляр к прямой 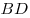 , восставленный в точке , восставленный в точке 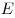 перпендикуляр к прямой перпендикуляр к прямой 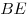 и биссектриса угла и биссектриса угла  пересекаются в одной точке. пересекаются в одной точке.
Фокусница Ната придумала многочлен 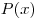 , при подстановке в который вместо , при подстановке в который вместо  натуральных чисел от 1 до 2002 получаются числа, делящиеся на 2003, тогда как натуральных чисел от 1 до 2002 получаются числа, делящиеся на 2003, тогда как 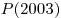 не делится на 2003. Раскройте секрет ее фокуса. не делится на 2003. Раскройте секрет ее фокуса.
Какое наибольшее число точек можно расположить в пространстве так, чтобы во всех образованных ими треугольниках ни один из углов не был меньше 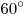 ? ?
Можно ли расставить в квадрате 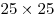 числа от 1 до 625 так, чтобы сумма чисел в каждой строке и в каждом столбце была бы простым числом? числа от 1 до 625 так, чтобы сумма чисел в каждой строке и в каждом столбце была бы простым числом?
Найдите длину отрезка, являющегося множеством значений функции 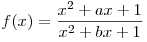 , где , где 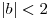 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
|

