|
Единый государственный экзамен по математике, 2009 год
Демонстрационная версия
Часть A
A1. Упростите выражение 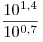 . .
A2. Вычислите: ![\sqrt[3]{{0,064 \cdot 27}} \sqrt[3]{{0,064 \cdot 27}}](/inc/pictures/941e3243f8c1635a3f85ae2469d085e7.png) . .
A3. Вычислите: 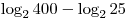 . .
A4. На одном из рисунков изображен график функции 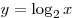 . Укажите номер этого рисунка. . Укажите номер этого рисунка.
A5. Найдите производную функции 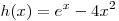 . .
A6. Найдите множество значений функции 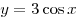 . .
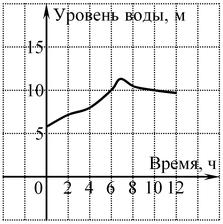 A7. На рисунке показано изменение уровня воды водохранилища в течение 12 часов во время паводка. Как только уровень воды превысил отметку 10 метров, через сливные отверстия в плотине начали сбрасывать воду до того момента, пока ее уровень понизился до отметки 10 метров. Определите, сколько часов длился сброс воды.
A7. На рисунке показано изменение уровня воды водохранилища в течение 12 часов во время паводка. Как только уровень воды превысил отметку 10 метров, через сливные отверстия в плотине начали сбрасывать воду до того момента, пока ее уровень понизился до отметки 10 метров. Определите, сколько часов длился сброс воды.
A8. Решите неравенство 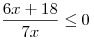 . .
A9. Решите уравнение 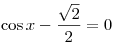 . .
A10. Решите неравенство 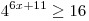 . .
Часть B
B1. Найдите 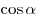 , если , если 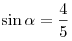 , и , и 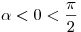 . .
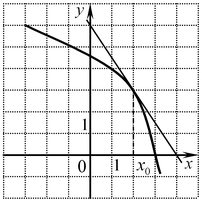 B2. На рисунке изображен график функции
B2. На рисунке изображен график функции  и касательная к нему в точке с абсциссой и касательная к нему в точке с абсциссой 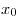 . Найдите значение производной в точке . Найдите значение производной в точке 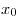 . .
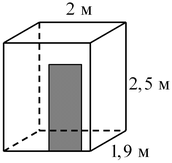 B3. Для оклейки стен ванной комнаты (см. рисунок) нужно приобрести керамическую плитку, причем плитка покупается с запасом в 10% от оклеиваемой площади. Ширина двери равна 0,75 м, высота — 2 м. Цена плитки 300 р. за 1 кв. м. Определите стоимость плитки, если стены решено оклеить полностью, от пола до потолка.
B3. Для оклейки стен ванной комнаты (см. рисунок) нужно приобрести керамическую плитку, причем плитка покупается с запасом в 10% от оклеиваемой площади. Ширина двери равна 0,75 м, высота — 2 м. Цена плитки 300 р. за 1 кв. м. Определите стоимость плитки, если стены решено оклеить полностью, от пола до потолка.
B4. Решите уравнение 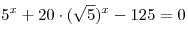 . (Если уравнение имеет более одного корня, то в бланке ответов запишите их произведение.) . (Если уравнение имеет более одного корня, то в бланке ответов запишите их произведение.)
 B5. Функция
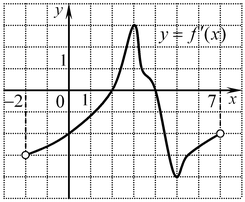
B5. Функция  определена на промежутке определена на промежутке 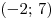 . На рисунке изображен график ее производной. Укажите точку минимума функции . На рисунке изображен график ее производной. Укажите точку минимума функции  на промежутке на промежутке 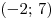 . .
B6. Вычислите значение выражения 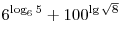 . .
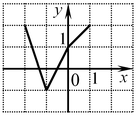 B7. Функция
B7. Функция  определена на всей числовой прямой и является периодической с периодом 3. На рисунке изображен график этой функции при определена на всей числовой прямой и является периодической с периодом 3. На рисунке изображен график этой функции при 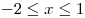 . Найдите значение выражения . Найдите значение выражения 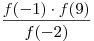 . .
B8. Найдите все значения  , при каждом из которых уравнение , при каждом из которых уравнение 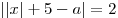 имеет ровно 3 корня. (Если значений a более одного, то в бланке ответов запишите их сумму.) имеет ровно 3 корня. (Если значений a более одного, то в бланке ответов запишите их сумму.)
B9. Объемы ежегодной добычи нефти первой, второй и третьей скважинами относятся как 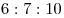 . Планируется уменьшить годовую добычу нефти из первой скважины на . Планируется уменьшить годовую добычу нефти из первой скважины на 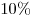 и из второй — тоже на и из второй — тоже на 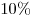 . На сколько процентов нужно увеличить годовую добычу нефти из третьей скважины, чтобы суммарный объем добываемой за год нефти не изменился? . На сколько процентов нужно увеличить годовую добычу нефти из третьей скважины, чтобы суммарный объем добываемой за год нефти не изменился?
B10. Концы отрезка 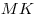 лежат на окружностях двух оснований цилиндра. Угол между прямой лежат на окружностях двух оснований цилиндра. Угол между прямой 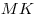 и плоскостью основания цилиндра равен и плоскостью основания цилиндра равен 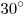 , , 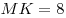 , площадь боковой поверхности цилиндра равна , площадь боковой поверхности цилиндра равна 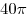 . Найдите периметр осевого сечения цилиндра. . Найдите периметр осевого сечения цилиндра.
B11. Средняя линия прямоугольной трапеции равна 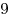 , а радиус вписанной в нее окружности равен , а радиус вписанной в нее окружности равен 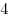 . Найдите большее основание трапеции. . Найдите большее основание трапеции.
Часть C
C1. Найдите наименьшее значение функции 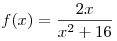 при при 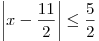 . .
C2. Найдите все значения  , при каждом из которых выражения , при каждом из которых выражения 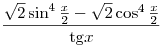 и и 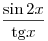 принимают равные значения. принимают равные значения.
C3. Найдите все значения 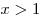 , при каждом из которых наибольшее из двух чисел , при каждом из которых наибольшее из двух чисел 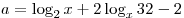 и и 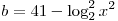 больше 5. больше 5.
C4. Около правильной пирамиды 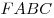 описана сфера, центр которой лежит в плоскости основания описана сфера, центр которой лежит в плоскости основания  пирамиды. Точка пирамиды. Точка  лежит на ребре лежит на ребре  так, что так, что 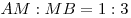 . Точка . Точка 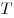 лежит на прямой лежит на прямой 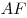 и равноудалена от точек и равноудалена от точек  и и  . Объем пирамиды . Объем пирамиды 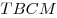 равен равен 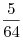 . Найдите радиус сферы, описанной около пирамиды . Найдите радиус сферы, описанной около пирамиды 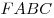 ? ?
C5. Найдите все значения параметра  , при каждом из которых уравнение , при каждом из которых уравнение
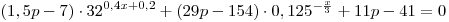
имеет ровно 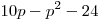 различных корней. различных корней.
Ответы к заданиям
| A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A8 |
A9 |
A10 |
| 3 |
3 |
4 |
4 |
2 |
2 |
4 |
2 |
2 |
2 |
| B1 |
B2 |
B3 |
B4 |
B5 |
B6 |
B7 |
B8 |
B9 |
B10 |
B11 |
 |
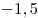 |
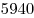 |
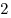 |
 |
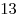 |
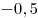 |
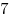 |
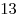 |
 |
 |
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
