|
Единый государственный экзамен по математике, 2006 год
Часть A
A1. Упростите выражение 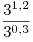 . .
A2. Найдите значение выражения 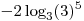 . .
A3. Вычислите: ![\sqrt[4]{{625 \cdot {\rm{0}}{\rm{,0081}}}} \sqrt[4]{{625 \cdot {\rm{0}}{\rm{,0081}}}}](/inc/pictures/7de61349a6b8c5ced0b8643f113107b4.png) . .
A4. На каком из следующих рисунков изображен график функции, возрастающей на промежутке ![[0;\, 2] [0;\, 2]](/inc/pictures/b4e5675ba2f02b6e6b0b4b6b582ee59a.png) ? ?
A5. Найдите множество значений функции 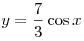 . .
A6. Найдите область определения функции 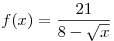 . .
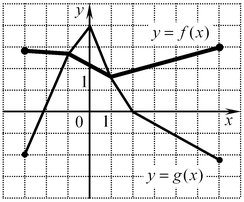 A7. На рисунке изображены графики функций
A7. На рисунке изображены графики функций  и и 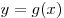 , заданных на промежутке , заданных на промежутке ![\left[ { - 3;\,6} \right] \left[ { - 3;\,6} \right]](/inc/pictures/996e55b9590b25f47d4ce2707ef5faed.png) . Укажите те значения . Укажите те значения  , для которых выполняется неравенство , для которых выполняется неравенство 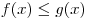 . .
A8. Найдите производную функции 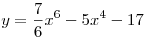 . .
A9. Решите уравнение 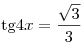 . .
A10. Решите неравенство 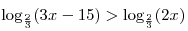 . .
Часть B
B1. Решите уравнение 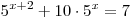 . .
B2. Решите уравнение 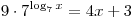 . .
B3. Найдите значение выражения 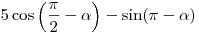 , если , если
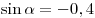 . .
B4. Вычислите: ![13\,\log _{9\sqrt[6]{3}}
(27\sqrt[6]{3}) 13\,\log _{9\sqrt[6]{3}}
(27\sqrt[6]{3})](/inc/pictures/9547baafe58960e5ec1469c20393fb2c.png) . .
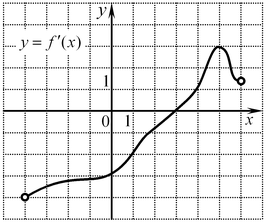 B5. К графику функции
B5. К графику функции  в точке с абсциссой в точке с абсциссой
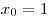 проведена касательная. Найдите ее угловой коэффициент, если на рисунке изображен график производной этой функции. проведена касательная. Найдите ее угловой коэффициент, если на рисунке изображен график производной этой функции.
B6. Найдите разность между наибольшим и наименьшим
значениями функции 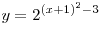 на отрезке на отрезке ![[- 3;\,0] [- 3;\,0]](/inc/pictures/1a8d3f23c03b88209a18c67b2371b09b.png) . .
B7. Решите уравнение
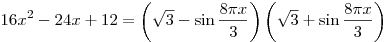 . .
B8. Найдите значение функции 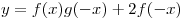 в точке в точке 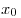 , если известно, что функция , если известно, что функция  — четная, функция — четная, функция 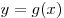 — нечетная, — нечетная, 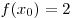 , , 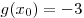 . .
B9. Объемы ежегодной добычи угля первой, второй и третьей шахтами относятся как 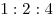 . Первая шахта планирует уменьшить годовую добычу угля на . Первая шахта планирует уменьшить годовую добычу угля на 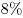 , а вторая — на , а вторая — на 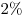 . На сколько процентов должна увеличить годовую добычу угля третья шахта, чтобы суммарный объем добываемого за год угля не изменился? . На сколько процентов должна увеличить годовую добычу угля третья шахта, чтобы суммарный объем добываемого за год угля не изменился?
B10. Основание прямой призмы 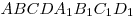 — параллелограмм — параллелограмм 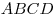 , в котором , в котором 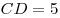 , , 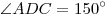 . Высота призмы равна . Высота призмы равна 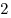 . Найдите тангенс угла между плоскостью основания призмы и плоскостью . Найдите тангенс угла между плоскостью основания призмы и плоскостью 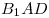 . .
B11. Найдите площадь равнобедренной трапеции, если ее средняя линия равна  , а косинус угла между диагональю и основанием равен , а косинус угла между диагональю и основанием равен 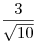 . .
Часть C
C1. Решите уравнение 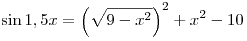 . .
С2. Найдите все значения  , при каждом из которых расстояние между соответствующими точками графиков функций , при каждом из которых расстояние между соответствующими точками графиков функций 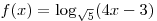 и и 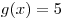 меньше, чем 1. меньше, чем 1.
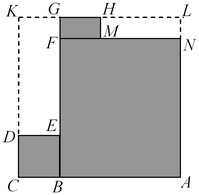 С3. Требуется разметить на земле участок
С3. Требуется разметить на земле участок 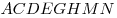 площадью 1200 площадью 1200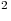 , состоящий из трех прямоугольных частей и имеющий форму, изображенную на рисунке, где , состоящий из трех прямоугольных частей и имеющий форму, изображенную на рисунке, где
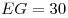 м, м, 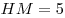 м, м, 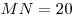 м и м и 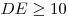 м. Найдите наименьшее значение периметра такого участка и
какие-либо значения длин м. Найдите наименьшее значение периметра такого участка и
какие-либо значения длин 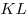 , , 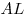 и и 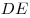 , при которых периметр является наименьшим. , при которых периметр является наименьшим.
C4. В пирамиде 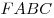 грани грани 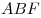 и и  перпендикулярны, перпендикулярны, 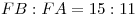 . Тангенс угла между прямой . Тангенс угла между прямой  и плоскостью и плоскостью 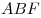 равен равен 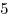 . Точка . Точка  выбрана на ребре выбрана на ребре  так, что так, что 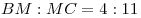 . Точка . Точка 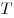 лежит на прямой лежит на прямой 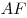 и равноудалена от точек и равноудалена от точек  и и  . Центр сферы, описанной около пирамиды . Центр сферы, описанной около пирамиды 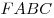 , лежит на ребре , лежит на ребре  ,
площадь этой сферы равна ,
площадь этой сферы равна 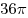 . Найдите объем пирамиды . Найдите объем пирамиды
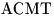 . .
С5. Найдите все значения  , при каждом из которых оба числа , при каждом из которых оба числа 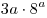 и и 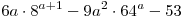 являются решениями неравенства являются решениями неравенства 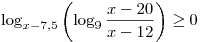 . .
Ответы к заданиям
| A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A8 |
A9 |
A10 |
| 1 |
2 |
4 |
1 |
1 |
1 |
2 |
1 |
4 |
3 |
| B1 |
B2 |
B3 |
B4 |
B5 |
B6 |
B7 |
B8 |
B9 |
B10 |
B11 |
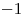 |
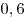 |
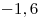 |
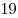 |
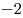 |
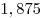 |
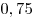 |
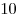 |
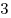 |
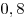 |
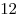 |
| C1 |
C2 |
C3 |
C4 |
C5 |
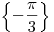 |
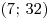 |
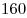 м, м, 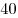 м, м, 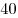 м, м, 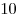 м м |
 |
 |
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
