|
Единый государственный экзамен по математике, 2003 год
Часть A
A1. Упростите выражение 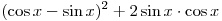 . .
A2. Упростите выражение 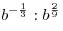 . .
A3. Вычислите: ![- \sqrt[5]{{0,016}} \cdot \sqrt[5]{{ - 0,02}} - \sqrt[5]{{0,016}} \cdot \sqrt[5]{{ - 0,02}}](/inc/pictures/12eb917ea53a7a68d4e9a8f73caefd68.png) . .
A4. Найдите значение выражения 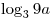 , если , если 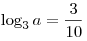 . .
A5. Найдите все решения уравнения 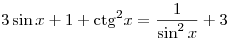 . .
A6. Укажите промежуток, которому принадлежит корень уравнения 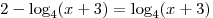 . .
A7. Решите неравенство 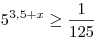 . .
A8. Решите неравенство 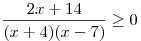 . .
A9. Укажите промежуток, которому принадлежат корни уравнения 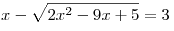 . .
 A10. Функция задана графиком. Укажите область определения этой функции.
A10. Функция задана графиком. Укажите область определения этой функции.
A11. Найдите область определения функции 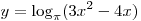 . .
A12. Найдите множество значений функции 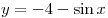 . .
A13. Укажите график функции, заданной формулой 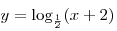 . .
A14. Найдите производную функции 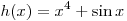 . .
A15. Для функции 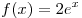 укажите
первообразную укажите
первообразную 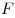 , график которой проходит через точку , график которой проходит через точку 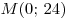 . .
A16. Найдите угловой коэффициент касательной, проведенной к графику функции 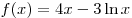 в его точке с абсциссой в его точке с абсциссой 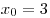 . .
Часть B
B1. Пусть 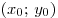 — решение системы уравнений — решение системы уравнений 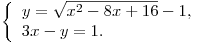 Найдите разность Найдите разность  . .
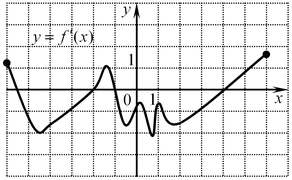 B2. На рисунке изображен график производной функции
B2. На рисунке изображен график производной функции 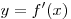 , заданной на отрезке , заданной на отрезке ![[ - 6;\,6] [ - 6;\,6]](/inc/pictures/6fc42039903455271b41c98b81a6ed37.png) . Исследуйте функцию . Исследуйте функцию  на монотонность и укажите в ответе число промежутков убывания. на монотонность и укажите в ответе число промежутков убывания.
B3. Найдите значение выражения 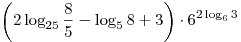 . .
B4. Найдите наименьшее целое значение функции 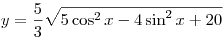 . .
B5. Определите число корней уравнения 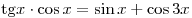 на отрезке на отрезке ![[0;\,2\pi ] [0;\,2\pi ]](/inc/pictures/ab38da89f1c5beeeb5fea26091c961f2.png) . .
B6. Найдите все значения  , при которых функция , при которых функция ![y = \sqrt[9]{{5x^2 - (2 - a)x + 2 - 4a}} y = \sqrt[9]{{5x^2 - (2 - a)x + 2 - 4a}}](/inc/pictures/4decd9a9eb95afa5debf596648951feb.png) имеет минимум в точке имеет минимум в точке 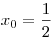 . .
B7. За год стипендия студента увеличилась на 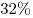 . В первом полугодии стипендия увеличилась на . В первом полугодии стипендия увеличилась на 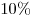 . Определите, на сколько процентов увеличилась стипендия во втором полугодии. . Определите, на сколько процентов увеличилась стипендия во втором полугодии.
B8. Одиннадцатый член арифметической прогрессии равен 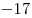 , а сумма первых сорока восьми членов равна , а сумма первых сорока восьми членов равна 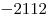 . Найдите сумму третьего, одиннадцатого и двадцатого членов
этой прогрессии. . Найдите сумму третьего, одиннадцатого и двадцатого членов
этой прогрессии.
B9. Основание пирамиды 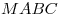 — треугольник — треугольник  , в котором , в котором 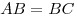 , , 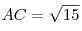 , , 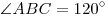 . Боковые ребра образуют с плоскостью основания равные углы. Найдите объем пирамиды, если . Боковые ребра образуют с плоскостью основания равные углы. Найдите объем пирамиды, если 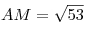 . .
B10. В треугольнике 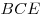 медиана медиана 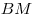 равна 3, равна 3, 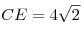 , , 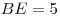 . Найдите сторону . Найдите сторону  . .
Часть C
C1. Решите уравнение 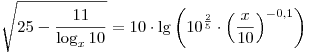 . .
C2. Найдите все значения  , при которых уравнение , при которых уравнение 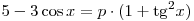 имеет хотя бы один корень. имеет хотя бы один корень.
C3. В правильную треугольную призму, площадь боковой поверхности которой равна 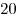 , вписан цилиндр. Расстояние между осью цилиндра и диагональю боковой грани призмы равно , вписан цилиндр. Расстояние между осью цилиндра и диагональю боковой грани призмы равно 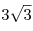 . Найдите объем цилиндра. . Найдите объем цилиндра.
C4. Найдите все значения  , при которых область определения функции , при которых область определения функции
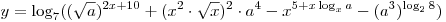
содержит ровно три натуральных числа.
Ответы к заданиям
| A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A8 |
A9 |
A10 |
A11 |
A12 |
A13 |
A14 |
A15 |
A16 |
| 1 |
4 |
1 |
2 |
4 |
3 |
4 |
2 |
3 |
2 |
2 |
3 |
4 |
3 |
2 |
3 |
| B1 |
B2 |
B3 |
B4 |
B5 |
B6 |
B7 |
B8 |
B9 |
B10 |
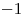 |
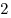 |
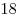 |
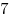 |
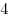 |
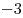 |
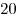 |
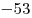 |
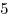 |
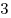 |
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
