|
Единый государственный экзамен по математике, 2002 год
Часть A
A1. Упростите выражение ![\frac{{\sqrt[4]{{32}}}}{{\sqrt[4]{4} \cdot \sqrt[4]{{64}}}} \frac{{\sqrt[4]{{32}}}}{{\sqrt[4]{4} \cdot \sqrt[4]{{64}}}}](/inc/pictures/b5cc83268b64343d0cffebe373696b30.png) . .
A2. Найдите значение выражения 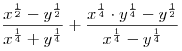 , если , если 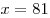 , , 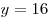 . .
A3. Упростите выражение 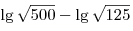 . .
A4. Упростите выражение 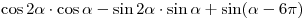 . .
A5. Укажите промежуток, которому принадлежит корень уравнения 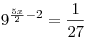 . .
A6. Решите неравенство 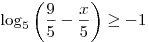 . .
A7. Найдите область определения функции 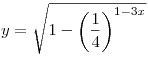 . .
A8. Найдите область значений функции 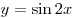 . .
A9. Укажите график четной функции.
A10. Найдите угловой коэффициент касательной, проведенной к графику функции 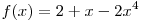 через его точку с абсциссой через его точку с абсциссой 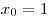 . .
A11. Найдите значение производной функции 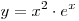 в точке в точке 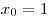 . .
A12. Укажите первообразную функции 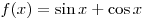 . .
A13. Решите уравнение 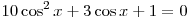 . .
Часть B
B1. Найдите минимум функции 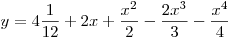 . .
B2. Вычислите площадь фигуры, ограниченной линиями 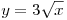 и и 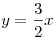 . .
B3. Сколько корней имеет уравнение 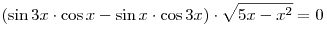 ? ?
B4. При каком наименьшем натуральном значении  функция функция 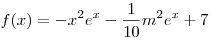 убывает на всей числовой прямой? убывает на всей числовой прямой?
B5. Пусть 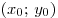 — решение
системы уравнений — решение
системы уравнений 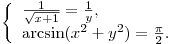 Вычислите значение суммы Вычислите значение суммы 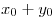 . .
B6. Найдите значение выражения 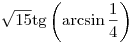 . .
B7. Найдите наименьшее значение функции 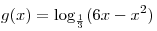 . .
B8. В прямоугольном треугольнике  с гипотенузой с гипотенузой 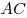 , равной , равной 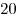 , проведена медиана , проведена медиана 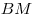 . Окружность, вписанная в треугольник . Окружность, вписанная в треугольник 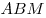 , касается медианы , касается медианы 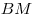 в точке в точке 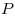 . Найдите катет . Найдите катет  , если , если 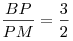 . .
B9. Основание пирамиды — квадрат со стороной
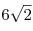 . Косинус угла наклона каждого бокового ребра к
плоскости основания равен . Косинус угла наклона каждого бокового ребра к
плоскости основания равен 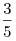 . Найдите объем
пирамиды. . Найдите объем
пирамиды.
Часть C
C1. Решите уравнение 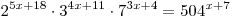 . .
C2. Найдите множество значений функции 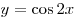 , заданной на отрезке , заданной на отрезке ![\left[ { - \arccos \frac{2}{5};\,\arccos \frac{2}{5}} \right] \left[ { - \arccos \frac{2}{5};\,\arccos \frac{2}{5}} \right]](/inc/pictures/32e96dcd8a004237e4f6cc4c9f6e83e3.png) . .
C3. При каких значениях  сумма сумма 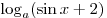 и и 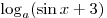 равна единице хотя бы при одном значении равна единице хотя бы при одном значении  ? ?
Ответы к заданиям
| A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A8 |
A9 |
A10 |
A11 |
A12 |
A13 |
| 4 |
3 |
1 |
1 |
4 |
2 |
3 |
1 |
1 |
2 |
4 |
2 |
4 |
| B1 |
B2 |
B3 |
B4 |
B5 |
B6 |
B7 |
B8 |
B9 |
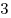 |
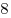 |
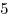 |
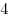 |
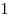 |
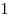 |
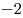 |
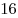 |
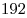 |
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
