|
Единый государственный экзамен по математике, 2005 год
Часть A
A1. Найдите значение выражения 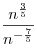 при при 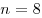 . .
Решение. Частное от делении степеней с одинаковыми основаниями есть степень с тем же основанием и показателем, равным разности показателей делимого и делителя:
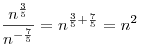 . .
При 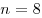 , получим: , получим: 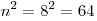 . .
Правильный ответ: 2.
A2. Упростите выражение ![\sqrt[7]{{2^{14} q^{14} }} \sqrt[7]{{2^{14} q^{14} }}](/inc/pictures/ccc655d3ac398efa7b24581e658574e1.png) . .
Решение. Поскольку ![\sqrt[7]{{ab}} =
\sqrt[7]{a}\sqrt[7]{b} \sqrt[7]{{ab}} =
\sqrt[7]{a}\sqrt[7]{b}](/inc/pictures/3f41944abd1b3891ab532ee8d1074111.png) , получаем: , получаем:
![\sqrt[7]{{2^{14} q^{14} }} = \sqrt[7]{{2^{14} }}\sqrt[7]{{q^{14}}} = 2^2 q^2 \sqrt[7]{{2^{14} q^{14} }} = \sqrt[7]{{2^{14} }}\sqrt[7]{{q^{14}}} = 2^2 q^2](/inc/pictures/0b6006350aa08e98f4ac2bbd16d7eb48.png) . .
Правильный ответ: 4.
A3. Вычислите значение выражения 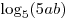 , если , если 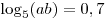 . .
Решение. Используя формулу преобразования логарифма произведения в сумму логарифмов, имеем
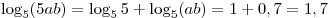 . .
Правильный ответ: 1.
A4. Упростите выражение 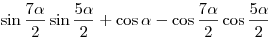 . .
Решение. Используя формулу 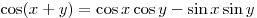 , получим: , получим:
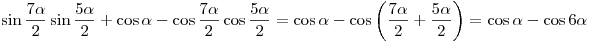 . .
Правильный ответ: 4.
A5. Найдите производную функции 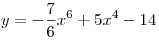 . .
Решение. Используя формулу 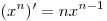 и правила дифференцирования, получим: и правила дифференцирования, получим:
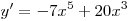 . .
Правильный ответ: 3.
A6. На каком из следующих рисунков функция, заданная графиком, убывает на промежутке ![[0;\,3] [0;\,3]](/inc/pictures/57c5760cc0aa28fd18e5d3d637e4d543.png) ? ?
Решение. Функция, график которой изображен на рисунке 1, убывает на отрезке ![[0;\,3] [0;\,3]](/inc/pictures/57c5760cc0aa28fd18e5d3d637e4d543.png) ; функция, график которой
изображен на рисунке 2, не является монотонной на отрезке ; функция, график которой
изображен на рисунке 2, не является монотонной на отрезке ![[0;\,3] [0;\,3]](/inc/pictures/57c5760cc0aa28fd18e5d3d637e4d543.png) ; функция, график которой изображен на рисунке 3, возрастает на отрезке ; функция, график которой изображен на рисунке 3, возрастает на отрезке ![[0;\,3] [0;\,3]](/inc/pictures/57c5760cc0aa28fd18e5d3d637e4d543.png) ; функция, график которой изображен на рисунке 4, не является монотонной на отрезке ; функция, график которой изображен на рисунке 4, не является монотонной на отрезке ![[0;\,3] [0;\,3]](/inc/pictures/57c5760cc0aa28fd18e5d3d637e4d543.png) . .
Правильный ответ: 1.
A7. Найдите множество значений функции 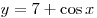 . .
Решение. В силу ограниченности функции косинус и свойств неравенств имеем:
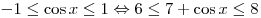 . .
Правильный ответ: 1.
A8. Решите уравнение 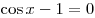 . .
Решение. Последовательно получаем:
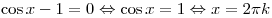 , , 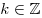
Правильный ответ: 4.
A9. Решите неравенство 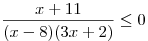 . .
Решение. Решим неравенство 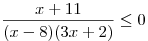 методом интервалов (см. рис.): методом интервалов (см. рис.):
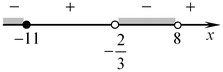
Правильный ответ: 4.
A10. Найдите область определения функции 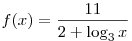 . .
Решение. Область определения функции задается соотношением 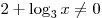 . Тогда: . Тогда:
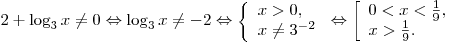
Правильный ответ: 4.
Часть B
B1. Решите уравнение 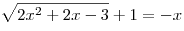 . .
Решение. Используем теорему равносильности 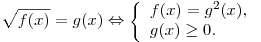
В нашем случае:
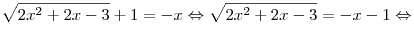
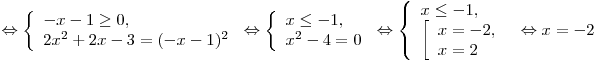 . .
Ответ: 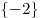 . .
B2. Решите уравнение 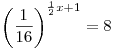 . .
Решение. Перейдем к одному основанию и воспользуемся монотонностью показательной функции:
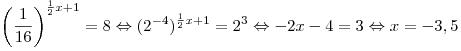 . .
Ответ: 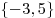 . .
B3. Точка движется по координатной прямой согласно закону 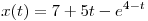 , где , где 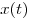 — координата точки в момент времени — координата точки в момент времени 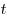 . Найдите скорость точки при . Найдите скорость точки при 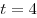 . .
Решение. Скорость точки в момент времени 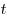 равна равна 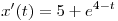 . При . При 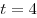 получаем получаем
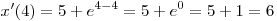 . .
Ответ: 6.
B4. Вычислите: ![(11,2\sqrt[3]{{64\sqrt 8 }} - 3,2\sqrt {8\sqrt[3]{{64}}} )^{\frac{6}{{11}}} (11,2\sqrt[3]{{64\sqrt 8 }} - 3,2\sqrt {8\sqrt[3]{{64}}} )^{\frac{6}{{11}}}](/inc/pictures/031a80a6fbe6d363e7e003daedec3ebd.png) . .
Решение. Применяя формулы ![\sqrt[n]{{a^m }} = a^{\frac{m}{n}} \sqrt[n]{{a^m }} = a^{\frac{m}{n}}](/inc/pictures/610dceeb3cbff0828cb37cb73bc1e395.png) , , 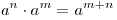 , , 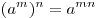 , последовательно получаем: , последовательно получаем:
![(11,2\sqrt[3]{{64\sqrt 8 }} - 3,2\sqrt {8\sqrt[3]{{64}}}
)^{\frac{6}{{11}}} = (11,2(8^2 \cdot 8^{\frac{1}{2}} )^{\frac{1}{3}}
- 3,2 \cdot (8 \cdot 8^{\frac{2}{3}} )^{\frac{1}{2}} )^{\frac{6}{{11}}} = (11,2\sqrt[3]{{64\sqrt 8 }} - 3,2\sqrt {8\sqrt[3]{{64}}}
)^{\frac{6}{{11}}} = (11,2(8^2 \cdot 8^{\frac{1}{2}} )^{\frac{1}{3}}
- 3,2 \cdot (8 \cdot 8^{\frac{2}{3}} )^{\frac{1}{2}} )^{\frac{6}{{11}}} =](/inc/pictures/93733f97476d775046284882b6592597.png)
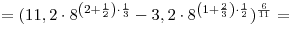
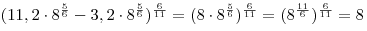 . .
Ответ: 8.
B5. Найдите значение функции 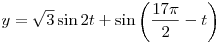 в точке в точке 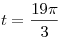 . .
Решение. Поскольку
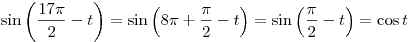 , ,
имеем:
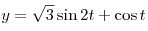 . .
Тогда
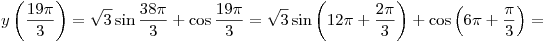
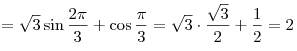 . .
Ответ: 2.
 B6. Функция
B6. Функция  определена на промежутке определена на промежутке 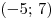 . График ее производной изображен на рисунке. Найдите промежутки убывания функции . График ее производной изображен на рисунке. Найдите промежутки убывания функции  . В ответе
укажите наибольшую из длин этих промежутков. . В ответе
укажите наибольшую из длин этих промежутков.
Решение. Интервалы убывания функции 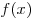 совпадают с интервалами, на которых ее производная отрицательна. Производная отрицательна на интервалах совпадают с интервалами, на которых ее производная отрицательна. Производная отрицательна на интервалах 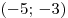 и и 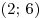 , длины которых соответственно равны , длины которых соответственно равны 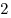 и и 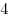 . Наибольшая длина – . Наибольшая длина – 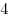 . .
Ответ: 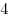 . .
B7. Найдите наибольший корень уравнения 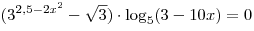 . .
Решение. Произведение равно нулю, если один из множителей равен нулю, а остальные при этом определены. Так как множитель 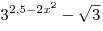 определен при любых значениях определен при любых значениях  , имеем: , имеем:
а) 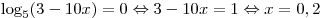 ; ;
б)
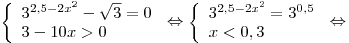
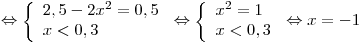 . .
Больший корень исходного уравнения — число 0,2.
Ответ: 0,2.
B8. Найдите значение функции 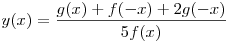 в точке в точке 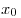 , если
известно, что функция , если
известно, что функция  четная, функция четная, функция 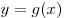 нечетная, нечетная, 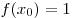 , , 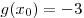 . .
Решение. В силу четности  имеем: имеем: 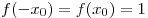 . В силу нечетности . В силу нечетности 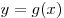 имеем: имеем: 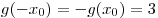 . Тогда . Тогда
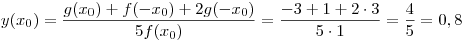 . .
Ответ: 0,8.
B9. Двум сотрудникам издательства поручили отредактировать рукопись объемом 560 страниц. Один сотрудник, отдав второму 80 страниц рукописи, взял остальные себе. Второй выполнил свою работу за время, в 8 раз меньшее, чем первый свою. Сколько страниц рукописи первый сотрудник должен был сразу отдать второму (взяв себе остальные), чтобы они, работая с прежней производительностью, выполнили свою работу за одинаковое время?
Решение (1 способ). Если второй сотрудник выполнил свою работу за
 дней, то он редактировал по дней, то он редактировал по 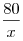 страниц
в день, а первый — по страниц
в день, а первый — по 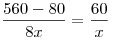 страниц в день. Поэтому первому сотруднику нужно было разделить 560 страниц в отношении страниц в день. Поэтому первому сотруднику нужно было разделить 560 страниц в отношении 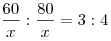 и отдать из них четыре части, т. е. и отдать из них четыре части, т. е. 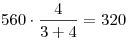 страниц, второму сотруднику. страниц, второму сотруднику.
Решение (2 способ). Второй сотрудник редактировал 80 страниц рукописи за время в восемь раз меньшее, чем первый 480 страниц рукописи. Если бы они работали с одной скоростью, то за время, в восемь раз меньшее, он должен был бы отредактировать 60 страниц. Значит, он работает со скоростью 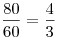 скорости первого
работника, и для того чтобы они закончили одновременно, работа должны
быть разделена между ними в отношении 4:3. Таким образом, первый сотрудник должен отдать второму скорости первого
работника, и для того чтобы они закончили одновременно, работа должны
быть разделена между ними в отношении 4:3. Таким образом, первый сотрудник должен отдать второму 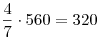 страниц. страниц.
Ответ: 320.
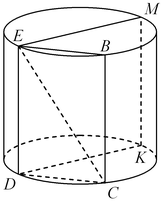 B10. Через образующую
B10. Через образующую  цилиндра проведено сечение цилиндра проведено сечение 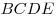 . Объем цилиндра равен . Объем цилиндра равен 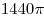 , , 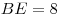 тангенс угла между прямой тангенс угла между прямой 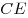 и плоскостью основания равен и плоскостью основания равен 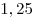 . Найдите площадь осевого сечения. . Найдите площадь осевого сечения.
Решение.
1. Имеем: 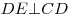 , , 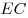 — наклонная, — наклонная, 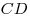 — ее проекция на плоскость основания, угол
— ее проекция на плоскость основания, угол 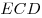 —
угол между прямой —
угол между прямой 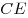 и плоскостью основания. Тогда, учитывая и плоскостью основания. Тогда, учитывая
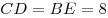 , из прямоугольного треугольника , из прямоугольного треугольника 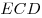 находим: находим: 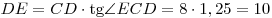 . .
2. Поскольку  и и  , имеем: , имеем: 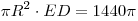 , откуда , откуда 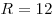 . .
3. Пусть 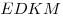 — осевое сечение цилиндра. Поскольку — осевое сечение цилиндра. Поскольку 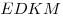 — прямоугольник и — прямоугольник и 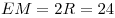 , имеем: , имеем:
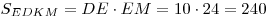 . .
Ответ: 240.
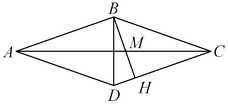 B11. Дан ромб
B11. Дан ромб 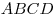 с острым углом с острым углом  . Высота . Высота
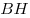 , проведенная к стороне , проведенная к стороне 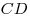 , пересекает диагональ , пересекает диагональ
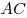 в точке в точке  . Найдите площадь треугольника . Найдите площадь треугольника 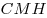 , если высота ромба равна , если высота ромба равна 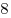 , а площадь ромба равна , а площадь ромба равна 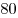 . .
Решение.
1. Найдем сторону ромба: 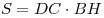 , откуда, , откуда, 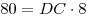 , , 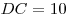 . .
2. Из прямоугольного треугольника 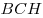 находим находим 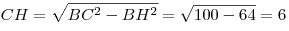 . .
3. В треугольнике 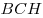 отрезок отрезок 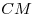 — биссектриса.
Биссектриса треугольника делит сторону, к которой она проведена на
отрезки, пропорциональные прилежащим сторонам: — биссектриса.
Биссектриса треугольника делит сторону, к которой она проведена на
отрезки, пропорциональные прилежащим сторонам:
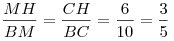 , откуда , откуда 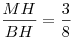 . .
4. Отрезок 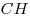 – общая высота треугольников – общая высота треугольников 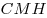 и и 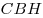 , следовательно, отношение площадей этих треугольников равно отношению их оснований , следовательно, отношение площадей этих треугольников равно отношению их оснований 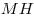 и и 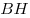 : :
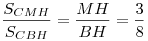 , откуда , откуда 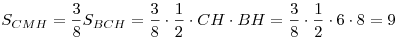 . .
Ответ: 9.
Часть C
C1. Найдите все значения  , для которых точки графика функции , для которых точки графика функции 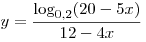 лежит ниже соответствующих точек графика функции лежит ниже соответствующих точек графика функции 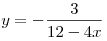 . .
Решение. Множество искомых значений  совпадает со множеством решений неравенства совпадает со множеством решений неравенства 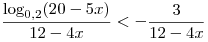 , решая которое, последовательно получаем: , решая которое, последовательно получаем:
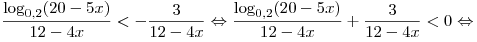
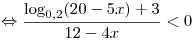 . .
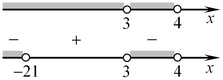 Решим последнее неравенство методом интервалов (на рисунке на первой оси отмечена область определения неравенства, задаваемая соотношениями
Решим последнее неравенство методом интервалов (на рисунке на первой оси отмечена область определения неравенства, задаваемая соотношениями 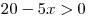 и и 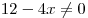 , а на второй — корни числителя и знаменателя): , а на второй — корни числителя и знаменателя):
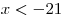 , , 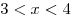 . .
Ответ: 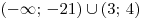 . .
C2. Решите уравнение 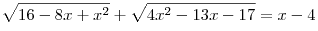 . .
Решение. Заметим, что 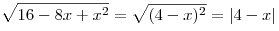 . Тогда: . Тогда:
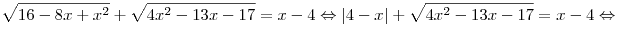
Поскольку правая часть полученного уравнения должна быть
неотрицательна, имеем условие: 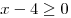 , откуда , откуда 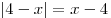 и уравнение принимает вид и уравнение принимает вид 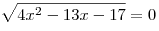 , где , где 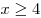 . (*) . (*)
Далее имеем:
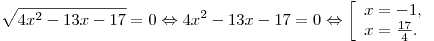
Условию (*) отвечает число 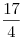 . .
Ответ: 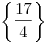
C3. Найдите все значения  , при каждом из которых наибольшее из двух чисел , при каждом из которых наибольшее из двух чисел 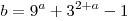 и и 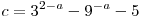 меньше 9. меньше 9.
Решение. Наибольшее из двух чисел меньше девяти тогда и только тогда, когда каждое из них меньше 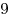 (если числа равны друг другу, наибольшим считается каждое из них). (если числа равны друг другу, наибольшим считается каждое из них).
Таким образом, имеем:
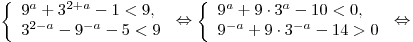
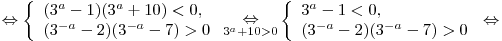
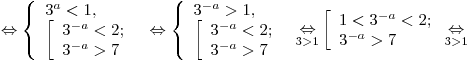
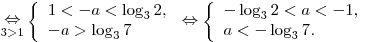
Ответ: 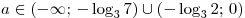 . .
C4. Отрезок 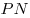 , равный , равный 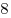 , – диаметр сферы. Точки , – диаметр сферы. Точки  и и 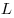 лежат на сфере так, что объем пирамиды лежат на сфере так, что объем пирамиды 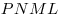 наибольший. Найдите площадь треугольника наибольший. Найдите площадь треугольника 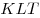 , где , где 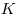 и и 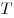 – середины ребер – середины ребер 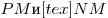 соответственно. соответственно.
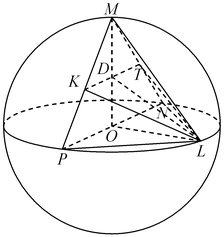 Решение. Примем треугольник
Решение. Примем треугольник 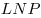 за основание пирамиды за основание пирамиды 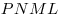 , а отрезок , а отрезок 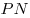 – за основание треугольника – за основание треугольника 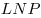 (см.рис). Тогда объем пирамиды (см.рис). Тогда объем пирамиды 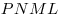 можно вычислить по формуле можно вычислить по формуле 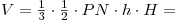 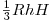 , где , где 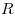 – радиус данной сферы, – радиус данной сферы, 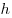 – высота треугольника – высота треугольника 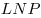 , проведенная из вершины , проведенная из вершины 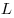 , , 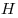 – высота пирамиды – высота пирамиды 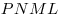 . Поскольку . Поскольку 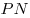 – диаметр данной сферы, а точка – диаметр данной сферы, а точка 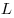 лежит на сфере, треугольник лежит на сфере, треугольник 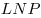 – прямоугольный треугольник, вписанный в окружность, радиус которой равен радиусу – прямоугольный треугольник, вписанный в окружность, радиус которой равен радиусу 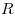 данной сферы. Следовательно, наибольшее значение высоты данной сферы. Следовательно, наибольшее значение высоты 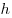 треугольника треугольника 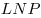 равно равно 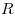 . Плоскость . Плоскость 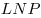 отсекает от данной сферы полусферу, следовательно, наибольшее расстояние от точек сферы до этой плоскости также равно радиусу сферы, откуда отсекает от данной сферы полусферу, следовательно, наибольшее расстояние от точек сферы до этой плоскости также равно радиусу сферы, откуда 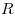 – наибольшее значение высоты – наибольшее значение высоты 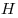 пирамиды пирамиды 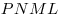 . Таким образом, пирамида . Таким образом, пирамида 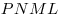 имеет наибольший объем, если треугольники имеет наибольший объем, если треугольники 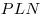 и и 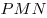 прямоугольные, равнобедренные треугольники с общей гипотенузой прямоугольные, равнобедренные треугольники с общей гипотенузой 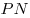 , лежащие во взаимно перпендикулярных плоскостях (см. рис.). , лежащие во взаимно перпендикулярных плоскостях (см. рис.).
Далее имеем:
1) Треугольники 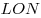 , , 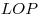 , , 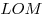 , , 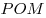 , , 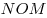 равны по двум катетам. равны по двум катетам.
2) Треугольники 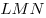 и и 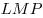 – равносторонние
треугольники со стороной – равносторонние
треугольники со стороной 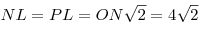 . Медианы . Медианы 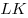 и и 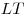 этих треугольников равны: этих треугольников равны: 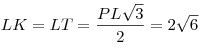 . .
3) Поскольку 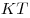 – средняя линия треугольника – средняя линия треугольника 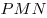 прямая
прямая 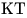 параллельна прямой параллельна прямой 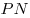 и и 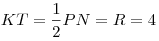 . В свою очередь, прямая . В свою очередь, прямая 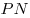 перпендикулярна двум пересекающимся прямым перпендикулярна двум пересекающимся прямым 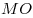 и и 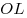 плоскости плоскости 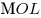 , значит, она перпендикулярна самой этой плоскости. Тогда прямая , значит, она перпендикулярна самой этой плоскости. Тогда прямая
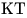 также перпендикулярна плоскости также перпендикулярна плоскости 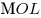 , а, значит, и
прямой , а, значит, и
прямой 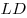 , лежащей в этой плоскости. , лежащей в этой плоскости.
4) Треугольник 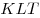 равнобедренный, и его высота равнобедренный, и его высота 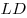 является медианой прямоугольного равнобедренного треугольника
является медианой прямоугольного равнобедренного треугольника 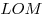 , откуда , откуда 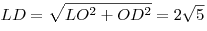 . .
Окончательно находим:
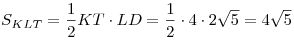 . .
Ответ: 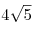 . .
C5. Даны два уравнения 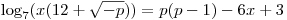 и и 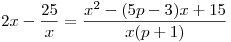 . Значение параметра . Значение параметра  выбирается так, что выбирается так, что 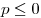 , , 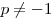 и число различных корней первого уравнения в сумме с числом и число различных корней первого уравнения в сумме с числом 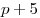 дает число различных корней второго уравнения. Решите первое уравнение
при каждом значении параметра, выбранном таким образом.
дает число различных корней второго уравнения. Решите первое уравнение
при каждом значении параметра, выбранном таким образом.
Решение. Умножив обе части уравнения 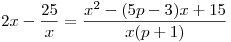 на общий знаменатель на общий знаменатель 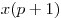 , получаем , получаем
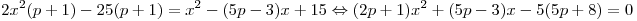 . .
По смыслу задачи  – целое отрицательное число, отличное от минус единицы и, кроме того, – целое отрицательное число, отличное от минус единицы и, кроме того,  не является корнем уравнения не является корнем уравнения 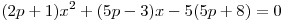 , следовательно, это уравнение равносильно данному уравнению. , следовательно, это уравнение равносильно данному уравнению.
Далее имеем:
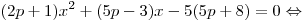
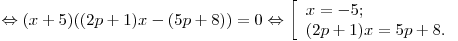
Таким образом, корнями рассматриваемого уравнения являются решения уравнения 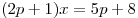 и число и число 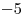 . Поскольку коэффициент при . Поскольку коэффициент при 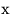 в уравнении в уравнении 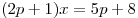 отличен от нуля при всех допустимых значениях параметра отличен от нуля при всех допустимых значениях параметра
 , данное уравнение имеет единственное решение, не равное , данное уравнение имеет единственное решение, не равное 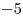 при целых значениях параметра при целых значениях параметра  . Поэтому число
различных корней второго уравнения равно 2. . Поэтому число
различных корней второго уравнения равно 2.
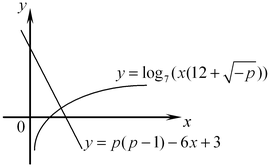 Рассмотрим теперь уравнение
Рассмотрим теперь уравнение 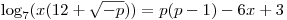 . Логарифмическая функция с основанием 7 – функция возрастающая и линейная функция . Логарифмическая функция с основанием 7 – функция возрастающая и линейная функция 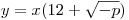 – возрастающая функция поскольку – возрастающая функция поскольку 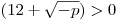 , следовательно, сложная функция , следовательно, сложная функция 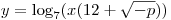 – также возрастающая функция. С другой
стороны, линейная функция – также возрастающая функция. С другой
стороны, линейная функция 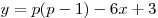 –
убывающая функция, так как –
убывающая функция, так как 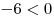 (см. рис). Таким
образом, данное уравнение имеет не более одного корня. Ясно, что в
нашем случае это корень есть. (см. рис). Таким
образом, данное уравнение имеет не более одного корня. Ясно, что в
нашем случае это корень есть.
По условию число различных корней первого уравнения в сумме с числом
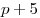 дает число различных корней второго уравнения, тогда дает число различных корней второго уравнения, тогда
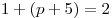 , откуда , откуда 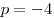 . .
Первое уравнение при 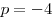 принимает вид принимает вид 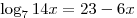 . Подбором находим . Подбором находим 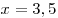 . Как показано
ранее, найденный корень единственный. . Как показано
ранее, найденный корень единственный.
Ответ: 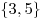 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
