|
Единый государственный экзамен по математике, 2002 год
Скачать pdf-файл.
Часть A
A1. Найдите значение выражения ![\sqrt[6]{{3^7 \cdot 4^5 }}
\cdot \sqrt[6]{{3^5 \cdot 4}} \sqrt[6]{{3^7 \cdot 4^5 }}
\cdot \sqrt[6]{{3^5 \cdot 4}}](/inc/pictures/dad94c27a575ed533090f05308342dfe.png) . .
|
1.
|
24
| |
2.
|
6
| |
3.
|
36
| |
4.
|
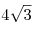 |
Решение. Пользуясь свойствами арифметического корня находим:
![\sqrt[6]{{3^7 \cdot 4^5 }} \cdot \sqrt[6]{{3^5 \cdot 4}} =
\sqrt[6]{{3^7 \cdot 4^5 \cdot 3^5 \cdot 4}} = \sqrt[6]{{3^{12}
\cdot 4^6 }} = \sqrt[6]{{(3^2 \cdot 4)^6 }} = 3^2 \cdot 4 = 36 \sqrt[6]{{3^7 \cdot 4^5 }} \cdot \sqrt[6]{{3^5 \cdot 4}} =
\sqrt[6]{{3^7 \cdot 4^5 \cdot 3^5 \cdot 4}} = \sqrt[6]{{3^{12}
\cdot 4^6 }} = \sqrt[6]{{(3^2 \cdot 4)^6 }} = 3^2 \cdot 4 = 36](/inc/pictures/5ccc6fef799d475467b3a8c29e9ad6e4.png) . .
Правильный ответ: 3.
A2. Найдите значение выражения 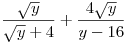 , при , при 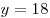 . .
Решение. Заметим, что 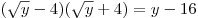 . Тогда . Тогда
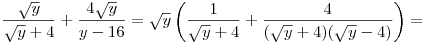
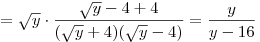 . .
При 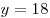 значение выражения равно значение выражения равно 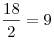 . .
Правильный ответ: 3.
A3. Укажите значение выражения 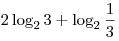 . .
Решение. Используя формулы логарифма степени и логарифма
произведения, находим:
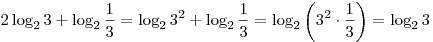 . .
Правильный ответ: 4.
A4. Упростите выражение 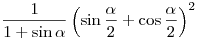 . .
Решение. Применяя основное тригонометрическое тождество и
формулу синуса двойного аргумента, получаем:
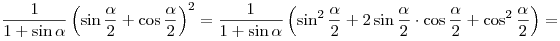
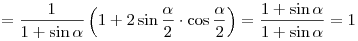 . .
Правильный ответ: 1.
A5. Укажите промежуток, которому принадлежит корень уравнения
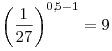 . .
Решение. Перейдем к степени с основанием 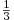 : :
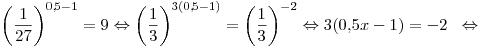 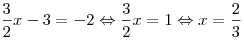 . .
Корень уравнения принадлежит промежутку 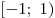 . .
Правильный ответ: 4.
A6. Решите неравенство 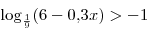 . .
Решение. Пользуясь свойством логарифмической функции, основание
которой меньше единицы, получаем:
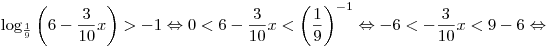
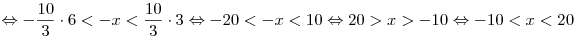 . .
Правильный ответ: 3.
A7. Найдите область определения функции ![y = \sqrt[4]{{1 -
7^{x^2 } \cdot 49^x }} y = \sqrt[4]{{1 -
7^{x^2 } \cdot 49^x }}](/inc/pictures/debbd75425a7ed95934052644987f0b0.png) . .
Решение. Область определения функции задается неравенством
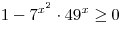 . Решим его: . Решим его:
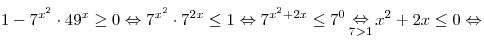
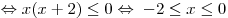 . .
Правильный ответ: 4.
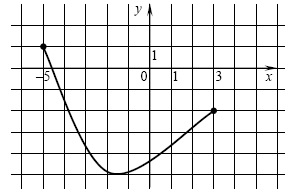 A8. Функция A8. Функция  задана графиком на отрезке задана графиком на отрезке
![[ - 5;\,\,3] [ - 5;\,\,3]](/inc/pictures/0a7e7212f6a74049e956b202e54ec870.png) . Укажите область ее значений. . Укажите область ее значений.
Решение. Значение функции — ордината проекции точки ее
графика на ось Oy. В нашем случае множество этих значений есть
отрезок ![[ - 5;\,\,1] [ - 5;\,\,1]](/inc/pictures/7edd2373124b03c3f06bc0b8a7e9b6c3.png) . .
Правильный ответ: 1.
A9. Найдите произведение корней уравнения 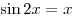 . .
|
1.
|
0
| |
2.
|
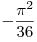 | |
3.
|
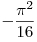 | |
4.
|
корней нет
|
Решение. Ясно, что число 0 — решение данного уравнения,
следовательно, сколько бы корней не имело данное уравнение,
произведение всех корней равно нулю.
Правильный ответ: 1.
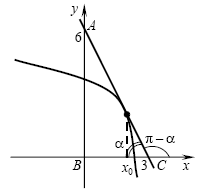 A10. На рисунке изображен график функции A10. На рисунке изображен график функции 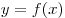 и касательная к нему в точке с абсциссой и касательная к нему в точке с абсциссой 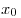 .
Найдите значение производной в точке .
Найдите значение производной в точке 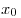 . .
Решение. Значение производной в точке касания равно тангенсу
угла наклона касательной к графику в этой точке, причем угол
отсчитывается от положительного направления оси абсцисс. Найдем тангенс
угла АСВ прямоугольного треугольника ABC (см. рис.):
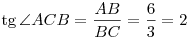 . Тогда тангенс угла наклона касательной есть . Тогда тангенс угла наклона касательной есть
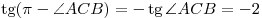 . .
Правильный ответ: 1.
A11. Найдите значение производной функции 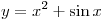 в точке в точке 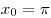 . .
Решение. Используя формулы 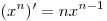 и и
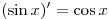 , получим: , получим:
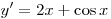 ; ;
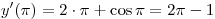 . .
Правильный ответ: 4.
A12. Укажите первообразную функции 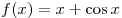 . .
Решение. Поскольку первообразной функции 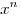 является является 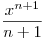 , а первообразной
функции , а первообразной
функции 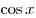 является является 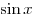 , получаем: , получаем:
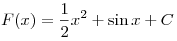 (в нашем случае (в нашем случае 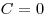 ). ).
Правильный ответ: 4.
A13. Решите уравнение 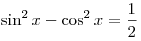 . .
Решение. Используя формулу косинуса двойного аргумента,
получаем:
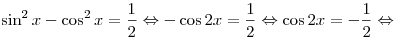
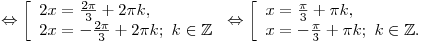
Правильный ответ: 4.
Часть B
B1. Найдите максимум функции 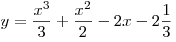 . .
Решение. Найдем производную:
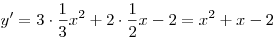 ; ;
Найдем нули производной:
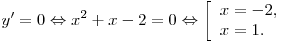
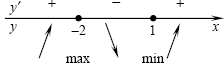 Знаки производной и промежутки монотонности функции показаны на
рисунке. Функция имеет максимум в точке Знаки производной и промежутки монотонности функции показаны на
рисунке. Функция имеет максимум в точке 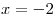 ,
следовательно, ,
следовательно,
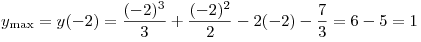 . .
Ответ: 1.
B2. Вычислите площадь фигуры, ограниченной линиями 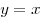 , , 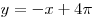 , , 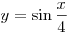 . .
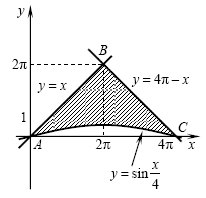 Решение. Построим эскизы графиков (см. рисунок). Площадь
заштрихованной фигуры равна разности площади треугольника ABC и
площади фигуры, ограниченной графиком функции Решение. Построим эскизы графиков (см. рисунок). Площадь
заштрихованной фигуры равна разности площади треугольника ABC и
площади фигуры, ограниченной графиком функции 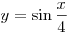 и отрезком и отрезком ![[0;\,\,4\pi ] [0;\,\,4\pi ]](/inc/pictures/b02d5620248abe47f58603a226b38ccd.png) оси абсцисс.
Координаты точки пересечения графиков оси абсцисс.
Координаты точки пересечения графиков 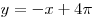 и и
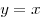 находятся из условия находятся из условия 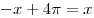 ,
откуда ,
откуда 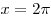 , , 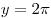 . Площадь треугольника
ABC равна: . Площадь треугольника
ABC равна:
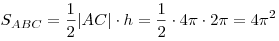 . .
Площадь криволинейной трапеции, ограниченной графиком функции 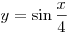 и отрезком и отрезком ![[0;\,\,4\pi ] [0;\,\,4\pi ]](/inc/pictures/b02d5620248abe47f58603a226b38ccd.png) оси абсцисс
равна: оси абсцисс
равна:
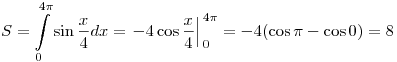 . .
Таким образом, искомая площадь равна:
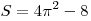 . .
Ответ: 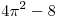 . .
B3. Сколько корней имеет уравнение 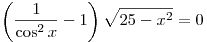 ? ?
Решение. Произведение равно нулю, если какой-то из множителей
равен нулю, а остальные при этом имеют смысл. Для нашего случая имеем:
либо а) 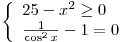 , либо б) , либо б) 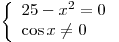 . .
а) 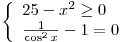 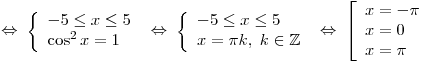 б) 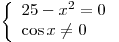 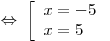
Таким образом, данное уравнение имеет пять корней.
Ответ: 5.
B4. При каком наибольшем значении a функция
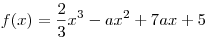 возрастает на всей
числовой прямой? возрастает на всей
числовой прямой?
Решение. Поскольку функция 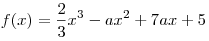 дифференцируема на всей числовой прямой, она
возрастает, если дифференцируема на всей числовой прямой, она
возрастает, если 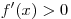 при любом значении x, за
исключением, может быть, «отдельных» точек, в которых при любом значении x, за
исключением, может быть, «отдельных» точек, в которых
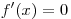 . .
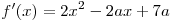 . .
Чтобы 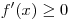 на всей числовой прямой, необходимо,
чтобы дискриминант квадратного трехчлена на всей числовой прямой, необходимо,
чтобы дискриминант квадратного трехчлена 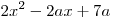 был неположителен: был неположителен:
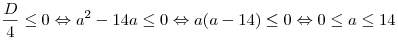 . .
Ответ: 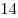 . .
B5. Пусть 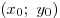 — решение системы — решение системы
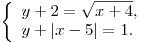 Найдите отношение Найдите отношение 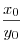 . .
Решение.
I способ.
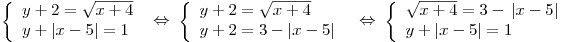 . .
Решим первое уравнение системы:
а) 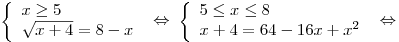
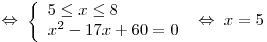 . .
б) 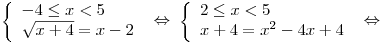
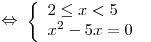 – система не имеет решений. – система не имеет решений.
Подставляя найденное значение x во второе уравнение системы,
получаем 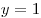 . Таким образом, пара (5; 1) –
единственное решение данной системы, откуда искомое отношение равно 5. . Таким образом, пара (5; 1) –
единственное решение данной системы, откуда искомое отношение равно 5.
II способ.
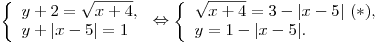
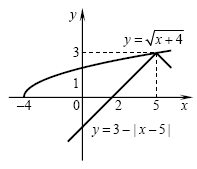 Решим уравнение (*) с помощью графиков функций Решим уравнение (*) с помощью графиков функций 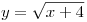 и и 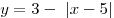 . Проверка подтверждает, что
«вершина» графика . Проверка подтверждает, что
«вершина» графика 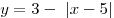 –
точка –
точка 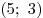 – принадлежит графику функции – принадлежит графику функции 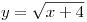 , следовательно, графики имеют ровно одну общую
точку – , следовательно, графики имеют ровно одну общую
точку – 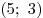 . Отсюда следует, что . Отсюда следует, что 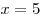 – единственное решение уравнения (*). – единственное решение уравнения (*).
Далее получаем:
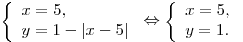
Таким образом, искомое отношение равно 5.
Ответ: 5.
B6. Найдите значение выражения 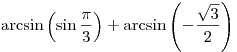 . .
Решение. Поскольку 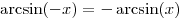 ,
получаем: ,
получаем:
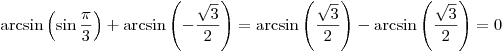 . .
Ответ: 0.
B7. Найдите наименьшее значение функции 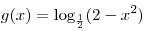 . .
Решение. Поскольку 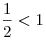 , функции , функции
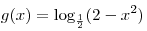 принимает свое
наименьшее значение в той точке, в которой функция принимает свое
наименьшее значение в той точке, в которой функция 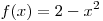 принимает свое наибольшее значение, т.е. в точке принимает свое наибольшее значение, т.е. в точке 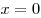 . Таким образом, наименьшее значение функции . Таким образом, наименьшее значение функции 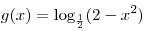 равно равно 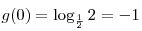 . .
Ответ: 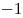 . .
B8. В равнобедренный треугольник PMK с основанием
MK вписана окружность с радиусом 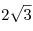 . Высота
PH делится точкой пересечения с окружностью в отношении . Высота
PH делится точкой пересечения с окружностью в отношении
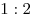 , считая от вершины P. Найдите периметр
треугольника PMK. , считая от вершины P. Найдите периметр
треугольника PMK.
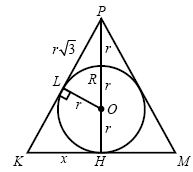 Решение. Решение.
I способ.
1. Поскольку PH делится точкой R пересечения с
окружностью в отношении 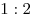 , имеем: , имеем:
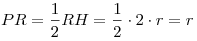 ; откуда ; откуда 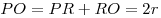 . .
2. Проведем 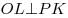 , , 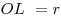 .
Поскольку в прямоугольном треугольнике PLO катет OL равен
половине гипотенузы PO, имеем .
Поскольку в прямоугольном треугольнике PLO катет OL равен
половине гипотенузы PO, имеем 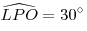 . Тогда . Тогда 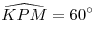 и и  – равносторонний треугольник. Тогда – равносторонний треугольник. Тогда
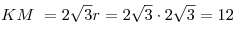 ,
откуда ,
откуда 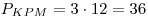 . .
II способ.
1 Поскольку PH делится точкой R пересечения с
окружностью в отношении 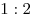 , имеем: , имеем:
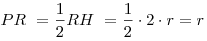 ; откуда ; откуда 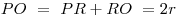 и и 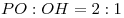 . .
2. Так как PMK – равнобедренный треугольник, его
высота PH является также и медианой, следовательно, точка
О – точка пересечения медиан треугольника РМК. Но
центр вписанной в треугольник окружности есть точка пересечения его
биссектрис. Поскольку точка пересечения медиан треугольника РМК
и точка пересечения его биссектрис совпадают, треугольник
 – равносторонний треугольник, откуда получаем – равносторонний треугольник, откуда получаем
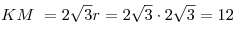 . .
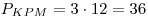 . .
Ответ: 36.
B9. В основании пирамиды лежит треугольник со сторонами
13, 12 и 5. Все боковые ребра наклонены к плоскости основания под углом
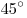 . Найдите объем пирамиды. . Найдите объем пирамиды.
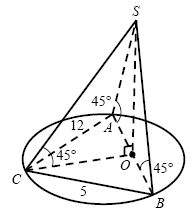 Решение. Введем обозначения, как показано на рисунке. Решение. Введем обозначения, как показано на рисунке.
1. Заметим, что в основании пирамиды лежит прямоугольный
треугольник (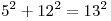 ), следовательно, его
площадь S равна половине произведения катетов: ), следовательно, его
площадь S равна половине произведения катетов:
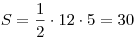 . .
2. Поскольку боковые ребра пирамиды одинаково наклонены к
плоскости основания, вершина пирамиды проектируется в центр окружности,
описанной около основания – в середину O гипотенузы
АВ.
3. Медиана СО прямоугольного треугольника АВС равна
радиусу описанной около него окружности – половине гипотенузы
АВ.
4. Треугольник SOC прямоугольный и равнобедренный
(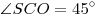 ), откуда ), откуда
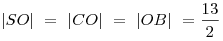 , ,
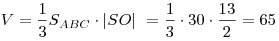 . .
Ответ: 65.
Часть C
C1. Решите уравнение 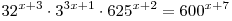 . .
Решение.
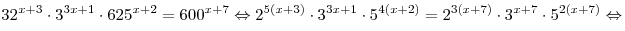
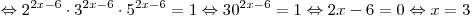 . .
Ответ: 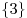 . .
C2. Найдите множество значений функции 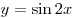 ,
если ,
если ![x \in \left[ {\mathop \arctg \frac{1}{2};\,\,{\mathop \arctg 3} \right] x \in \left[ {\mathop \arctg \frac{1}{2};\,\,{\mathop \arctg 3} \right]](/inc/pictures/d48d9428a7c3080e33b7c337e3b05bdb.png) . .
Решение.
 1. Пусть 1. Пусть 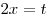 . Тогда множество значений функции . Тогда множество значений функции 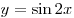 на отрезке на отрезке ![\left[ {\mathop \arctg \frac{1}{2};\,\,{\mathop \arctg 3} \right] \left[ {\mathop \arctg \frac{1}{2};\,\,{\mathop \arctg 3} \right]](/inc/pictures/f508649dab12a03ebc82d0ce0873ca09.png) совпадает с множеством значений функции совпадает с множеством значений функции 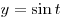 на
отрезке на
отрезке ![\left[ {2 \mathop \arctg \frac{1}{2};\,\,{2 \mathop \arctg 3} \right] \left[ {2 \mathop \arctg \frac{1}{2};\,\,{2 \mathop \arctg 3} \right]](/inc/pictures/d3bdce38f62130a0770546a85fa0bd67.png) . .
Так как 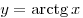 убывающая
функция убывающая
функция 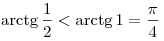 , , 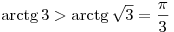 , откуда , откуда 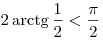 , , 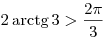 . .
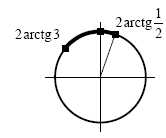
2. Изобразим отрезок ![\left[ {2 \mathop \arctg \frac{1}{2};\,\,{2 \mathop \arctg 3} \right] \left[ {2 \mathop \arctg \frac{1}{2};\,\,{2 \mathop \arctg 3} \right]](/inc/pictures/d3bdce38f62130a0770546a85fa0bd67.png) на
единичной окружности (см. рисунок). на
единичной окружности (см. рисунок).
Функция 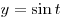 возрастает на отрезке возрастает на отрезке ![\left[
{2 \mathop \arctg \frac{1}{2};\,\,\frac{\pi }{2}}
\right] \left[
{2 \mathop \arctg \frac{1}{2};\,\,\frac{\pi }{2}}
\right]](/inc/pictures/e7c22304e098bf06b027a51e4645cb53.png) и убывает на отрезке и убывает на отрезке ![\left[ {\frac{\pi
}{2};\,\,2 \mathop \arctg 3} \right] \left[ {\frac{\pi
}{2};\,\,2 \mathop \arctg 3} \right]](/inc/pictures/8dfeed39ff9e2c92b234e02305c6ec92.png) ,
следовательно, свое наибольшее значение она принимает в точке ,
следовательно, свое наибольшее значение она принимает в точке 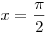 , а наименьшее – на одном из концов отрезка , а наименьшее – на одном из концов отрезка
![\left[ {2 \mathop \arctg \frac{1}{2};\,\,2 \mathop \arctg 3} \right] \left[ {2 \mathop \arctg \frac{1}{2};\,\,2 \mathop \arctg 3} \right]](/inc/pictures/bca53faa65949da61d7de8414972221d.png) . .
3. Вычислим эти значения:
а) наибольшее значение функции: 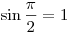 ; ;
б) поскольку 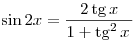 , имеем , имеем
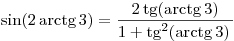 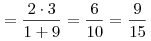 , ,
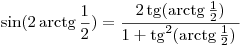 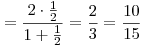 . .
Таким образом, 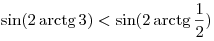 , откуда 0,6 –
наименьшее значение функции. , откуда 0,6 –
наименьшее значение функции.
Поскольку функция 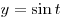 непрерывна на отрезке непрерывна на отрезке
![\left[ {2 \mathop \arctg \frac{1}{2};\,\,2 \mathop \arctg 3} \right] \left[ {2 \mathop \arctg \frac{1}{2};\,\,2 \mathop \arctg 3} \right]](/inc/pictures/bca53faa65949da61d7de8414972221d.png) ,
множество ее значений есть отрезок ,
множество ее значений есть отрезок ![\left[ {\sin (2 \mathop \arctg 3);\;\sin \frac{\pi }{2}} \right] \left[ {\sin (2 \mathop \arctg 3);\;\sin \frac{\pi }{2}} \right]](/inc/pictures/0540ba1b51c361cc28f51872ecf11f16.png) , т.е. отрезок , т.е. отрезок
![[0,\!6;\;1] [0,\!6;\;1]](/inc/pictures/175163b565e836784b884c5cfc5886e7.png) . .
.
Ответ: ![[0,\!6;\;1] [0,\!6;\;1]](/inc/pictures/175163b565e836784b884c5cfc5886e7.png) . .
C3. При каких значениях a сумма 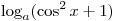 и и 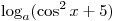 равна 1 хотя бы
при одном значении x? равна 1 хотя бы
при одном значении x?
Решение.
Требуется найти значения параметра a такие, что уравнение
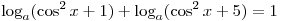 имеет
хотя бы одно решение. Поскольку имеет
хотя бы одно решение. Поскольку 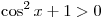 и и
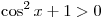 , имеем , имеем
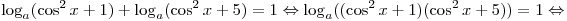
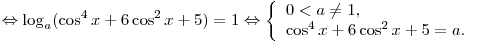
Уравнение 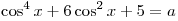 имеет решения, если a принадлежит множеству
значений функции имеет решения, если a принадлежит множеству
значений функции 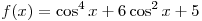 ,
совпадающему со множеством значений функции ,
совпадающему со множеством значений функции 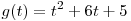 на отрезке на отрезке ![[0;\,\,1] [0;\,\,1]](/inc/pictures/166aa5a4cae3e47dad39d2e6f77ffdb3.png) . .
Поскольку абсцисса вершины 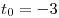 параболы параболы 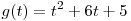 меньше нуля, функция меньше нуля, функция 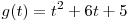 возрастает на отрезке возрастает на отрезке ![[0;\,\,1] [0;\,\,1]](/inc/pictures/166aa5a4cae3e47dad39d2e6f77ffdb3.png) и множество ее
значений на этом отрезке есть отрезок и множество ее
значений на этом отрезке есть отрезок ![[g(0);\;g(1)] [g(0);\;g(1)]](/inc/pictures/e87d046a8053a570bb0645613d3cf0ea.png) , т.е.
отрезок , т.е.
отрезок ![[5;\,\,12] [5;\,\,12]](/inc/pictures/c094431d1c8f51f5ce93e25acebcfc87.png) . Таким образом, искомыми значениями
параметра являются все числа a, такие, что . Таким образом, искомыми значениями
параметра являются все числа a, такие, что 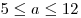 . .
Ответ: ![[5;\,\,12] [5;\,\,12]](/inc/pictures/c094431d1c8f51f5ce93e25acebcfc87.png) . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
