|
Единый государственный экзамен по математике, 2003 год
Скачать pdf-файл.
Часть A
A1. Упростите выражение 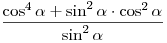 . .
Решение. Используя основное тригонометрическое тождество,
получаем:
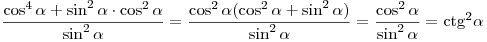 . .
Правильный ответ: 3.
A2. Представьте выражение 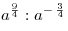 в виде степени с основанием a. в виде степени с основанием a.
Решение. На основании свойств степени имеем:
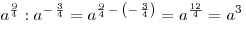 . .
Правильный ответ: 4.
A3. Вычислите ![\sqrt[3]{{125 \cdot 0,027}} \sqrt[3]{{125 \cdot 0,027}}](/inc/pictures/5bbb45ef0de029a9d32f318bbfd8295f.png) . .
|
1.
|
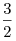 | |
2.
|
15
| |
3.
|
0,015
| |
4.
|
0,15
|
Решение. Применяя свойства корня последовательно получаем:
![\sqrt[3]{{125 \cdot 0,027}} = \sqrt[3]{{5^3 \cdot 3^3 \cdot
\left( {\frac{1}{{10}}} \right)^3 }} = 5 \cdot 3 \cdot \frac{1}{{10}} =
\frac{3}{2} \sqrt[3]{{125 \cdot 0,027}} = \sqrt[3]{{5^3 \cdot 3^3 \cdot
\left( {\frac{1}{{10}}} \right)^3 }} = 5 \cdot 3 \cdot \frac{1}{{10}} =
\frac{3}{2}](/inc/pictures/9f378a25fb4bafb53aa6793932dba200.png) . .
Правильный ответ: 1.
A4. Найдите значение выражения 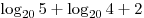 . .
Решение. Используя формулу преобразования суммы логарифмов в
логарифм произведения, получаем:
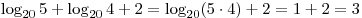 . .
Правильный ответ: 3.
A5. Найдите все решения уравнения 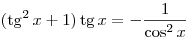 . .
Решение. Применив формулу 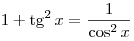 , получим: , получим:
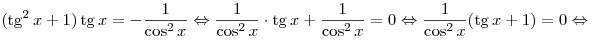
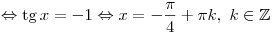 . .
Правильный ответ: 3.
A6. Укажите промежуток, которому принадлежит корень уравнения
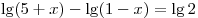 . .
Решение. Решим уравнение
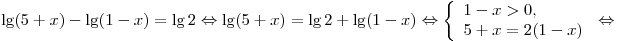 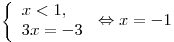 . .
Таким образом, корень уравнение
принадлежит промежутку 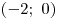 . .
Правильный ответ: 1.
A7. Решите неравенство 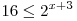 . .
Решение. По свойству показательной функции с основанием большим
единицы
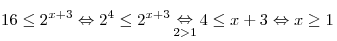 . .
Правильный ответ: 4.
A8. Определите число целых решений неравенства 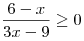 . .
Решение. Решим неравенство методом интервалов:
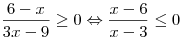
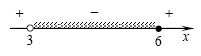
На промежутке ![(3;\,\,6] (3;\,\,6]](/inc/pictures/901873cc8e54c5febd0bb878dc83cda5.png) есть три целых решения: 4, 5, 6. есть три целых решения: 4, 5, 6.
Правильный ответ: 3.
A9. Укажите промежуток, которому принадлежат корни уравнения
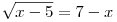 . .
Решение.
I способ. Используя теорему равносильности 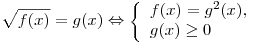 , получим: , получим:
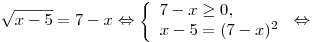
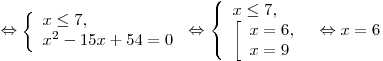 . .
II способ. Приведем уравнение к квадратному относительно 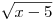 : :
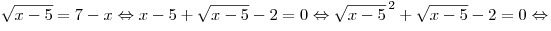
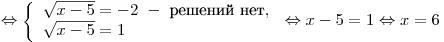
Таким образом, корень уравнения
принадлежит промежутку ![[5,\!5;\,\,6,\!3] [5,\!5;\,\,6,\!3]](/inc/pictures/535fbf4e4282cdc77b0033e60baa23eb.png) . .
Правильный ответ: 2.
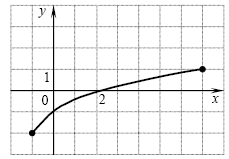 A10. Функция задана графиком. Укажите область определения этой
функции. A10. Функция задана графиком. Укажите область определения этой
функции.
Решение. Область определения функции есть множество значений ее
аргумента x. В нашем случае, это отрезок ![[ -
1;\,\,7] [ -
1;\,\,7]](/inc/pictures/655bdbd44072147924a0477819cc3db1.png) . .
Правильный ответ: 4.
A11. Найдите область определения функции 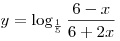 . .
Решение. Область определения функции задается неравенством
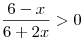 . Решим его методом интервалов: . Решим его методом интервалов:
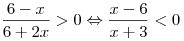
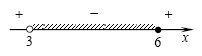
Правильный ответ: 1.
A12. Найдите множество значений функции 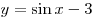 . .
Решение. В силу ограниченности функции синус и свойств
неравенств:
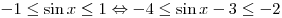 . .
Правильный ответ: 1.
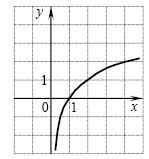 A13. График какой из перечисленных функций изображен на
рисунке? A13. График какой из перечисленных функций изображен на
рисунке?
Решение. На рисунке изображен график функции 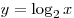 . .
Правильный ответ: 3.
A14. Найдите производную функции 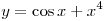 . .
Решение. Используя формулы 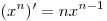 и и
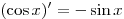 , получим: , получим:
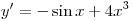 . .
Правильный ответ: 1.
A15. Найдите первообразную функции 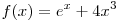 , если известно, что , если известно, что 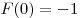 . .
Решение. Найдем множество первообразных 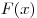 : :
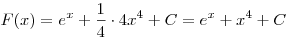 . .
Найдем C:
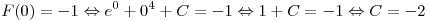 . .
Таким образом,
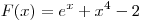 . .
Правильный ответ: 2.
A16. Найдите угловой коэффициент касательной, проведенной
к графику функции 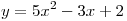 в его точке с абсциссой в его точке с абсциссой
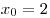 . .
Решение. Угловой коэффициент касательной к графику функции в
некоторой точке равен значению производной функции в этой точке:
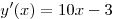 ; ;
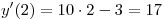 . .
Правильный ответ: 2.
Часть B
B1. Пусть 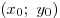 — решение системы — решение системы
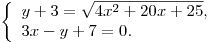 Найдите произведение Найдите произведение 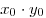 . .
Решение. Решим систему
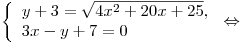
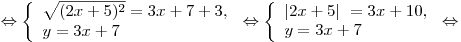
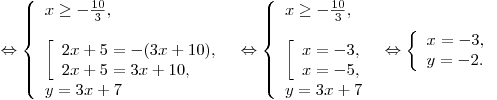
Таким образом, произведением
решений системы будет являться число 6.
Ответ: 6.
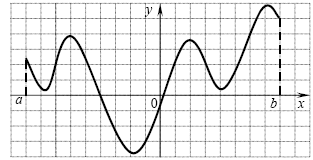 B2. На рисунке изображен график производной функции B2. На рисунке изображен график производной функции
 , заданной на отрезке , заданной на отрезке ![[a;\,\,b] [a;\,\,b]](/inc/pictures/bdae212ad71592a3e4f39c68268d7388.png) . Исследуйте функцию . Исследуйте функцию  на монотонность и в ответе
укажите число промежутков возрастания. на монотонность и в ответе
укажите число промежутков возрастания.
Решение. Данная функция возрастает на тех промежутках, на
которых производная этой функции неотрицательна. В нашем случае таких
промежутков 2.
Ответ: 2.
B3. Найдите значение выражения ![(\log _{\sqrt[5]{5}} \sqrt
5 + \log _3 48 - \log _3 16) \cdot 15^{\log _{15} 4} (\log _{\sqrt[5]{5}} \sqrt
5 + \log _3 48 - \log _3 16) \cdot 15^{\log _{15} 4}](/inc/pictures/1061c427526465df97b1ae8e7870b605.png) . .
Решение.
![(\log _{\sqrt[5]{5}} \sqrt 5 + \log _3 48 - \log _3 16) \cdot
15^{\log _{15} 4} = \left( {\log _{5^{\frac{1}{5}} } 5^{\frac{1}{2}}
+ \log _3 \frac{{48}}{{16}}} \right) \cdot 4 =
(\log _{\sqrt[5]{5}} \sqrt 5 + \log _3 48 - \log _3 16) \cdot
15^{\log _{15} 4} = \left( {\log _{5^{\frac{1}{5}} } 5^{\frac{1}{2}}
+ \log _3 \frac{{48}}{{16}}} \right) \cdot 4 =](/inc/pictures/872f1aeb2c2523734f48c22d54dfe774.png)
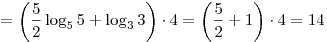 . .
Ответ: 14.
B4. Найдите наибольшее целое значение функции 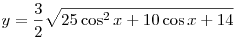 . .
Решение. Наибольшее значение функции y достигается при
наибольшем значении подкоренного выражения 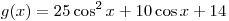 , т.е. при наибольшем значении квадратного
трехчлена , т.е. при наибольшем значении квадратного
трехчлена 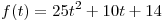 на отрезке на отрезке ![[ -
1;\,\,1] [ -
1;\,\,1]](/inc/pictures/eb34300e7789a73290ce402c8c22bf32.png) . .
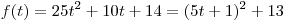 . .
![\mathop {\max }\limits_{[ - 1;\,\,1]} f(t) = f(1) = 6^2 + 13 =
49 \mathop {\max }\limits_{[ - 1;\,\,1]} f(t) = f(1) = 6^2 + 13 =
49](/inc/pictures/fd4254ab463c16e41146abbe1751ebfb.png) . .
Тогда
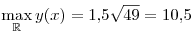 . .
Ответ: 10,5.
B5. Укажите число корней уравнения 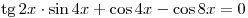 на промежутке на промежутке ![[0;\,\,2\pi ] [0;\,\,2\pi ]](/inc/pictures/80abb57551c523cbd1bef96fc47c030c.png) . .
Решение. Упростим выражение 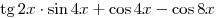 : :
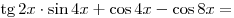 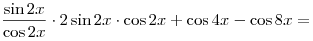
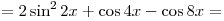 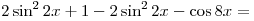 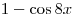 , где , где 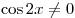 . .
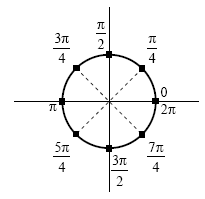 Решим систему Решим систему
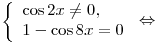
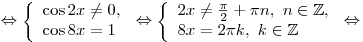
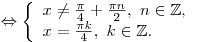 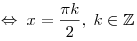 . .
На промежутке ![[0;\,\,2\pi
] [0;\,\,2\pi
]](/inc/pictures/37618fc050cccc81cacab56d8a0c3c58.png) решениями являются 0, решениями являются 0, 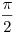 , , 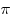 , , 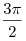 , , 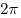 . .
Ответ: 5.
B6. При каком значении a функция ![y = \sqrt[5]{{ax^2
+ 15x - 1}} y = \sqrt[5]{{ax^2
+ 15x - 1}}](/inc/pictures/3bab021edab9b41360609ffce908143d.png) имеет максимум в точке имеет максимум в точке 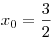 ? ?
Решение. Функция 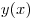 имеет максимум в той же точке,
что и фнкция имеет максимум в той же точке,
что и фнкция 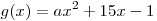 , которая имеет максимум
в точке , которая имеет максимум
в точке 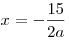 только при отрицательных
значений старшего коэффициента a. Решим уравнение только при отрицательных
значений старшего коэффициента a. Решим уравнение
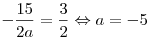 . .
Ответ: 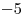 . .
B7. К 120 г раствора, содержащего 80% соли, добавили 480 г
раствора, содержащего 20% той же соли. Сколько процентов соли
содержится в получившемся растворе?
Решение. В первом растворе находится 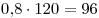 граммов, а во втором граммов, а во втором 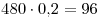 граммов
соли. Масса сухого вещества после сливания стала граммов
соли. Масса сухого вещества после сливания стала 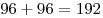 граммов, масса растворов граммов, масса растворов 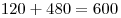 граммов. Тогда процентное содержание граммов. Тогда процентное содержание 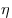 соли в полученном
растворе есть соли в полученном
растворе есть
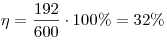 . .
Ответ: 32%.
B8. Десятый член арифметической прогрессии равен 19, а
сумма первых пятидесяти членов равна 2500. Найдите сумму третьего,
двенадцатого и двадцатого членов этой прогрессии.
Решение. Поскольку 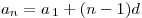 и и
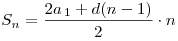 , имеем
систему , имеем
систему
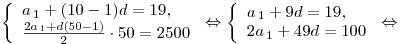
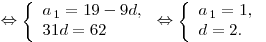
Таким образом,
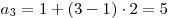 , ,
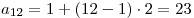 , ,
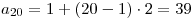 . .
Искомая сумма равна
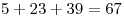 . .
Ответ: 67.
B9. Вычислите объем правильной треугольной пирамиды,
высота которой равна 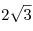 , а все плоские углы при
вершине прямые. , а все плоские углы при
вершине прямые.
Решение.
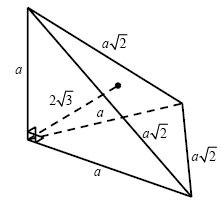 1. Пусть боковые ребра пирамиды имеют длину a. Тогда длина
стороны ее основания равна 1. Пусть боковые ребра пирамиды имеют длину a. Тогда длина
стороны ее основания равна 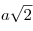 . Если за основание
принять одну из боковых граней пирамиды, то объем пирамиды равен . Если за основание
принять одну из боковых граней пирамиды, то объем пирамиды равен
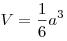 (см. рисунок). (см. рисунок).
2. С другой стороны
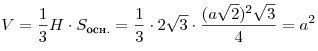 . .
3. Решая уравнение 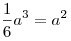 , находим , находим 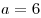 , откуда , откуда 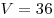 . .
Ответ: 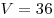 . .
B10. Найдите основание равнобедренного треугольника, если
угол при основании равен 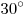 , а взятая внутри
треугольника точка находится на одинаковом расстоянии, равном 3, от
боковых сторон и на расстоянии , а взятая внутри
треугольника точка находится на одинаковом расстоянии, равном 3, от
боковых сторон и на расстоянии 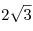 от основания. от основания.
Решение.
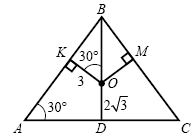 1. Введем обозначения, как показано на рисунке. Поскольку точка
O равноудалена от боковых сторон, она принадлежит BD
— биссектрисе, а, следовательно, медиане и высоте данного
треугольника. 1. Введем обозначения, как показано на рисунке. Поскольку точка
O равноудалена от боковых сторон, она принадлежит BD
— биссектрисе, а, следовательно, медиане и высоте данного
треугольника.
2. Треугольники ABD и OKB — подобны ( BKO = BKO =  BDA = 90° и BDA = 90° и  ABD — общий), следовательно, ABD — общий), следовательно, 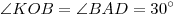 . .
Рассмотрим треугольник KBO:
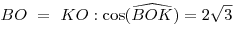 , ,
следовательно,
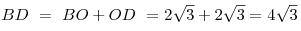 . .
3. Из прямоугольного треугольника ABD получаем
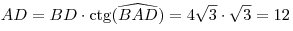 , и поскольку , и поскольку
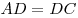 , , 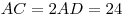 . .
Ответ: 24.
Часть C
C1. Решите уравнение 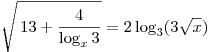 . .
Решение.
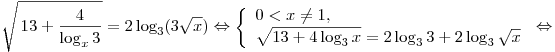
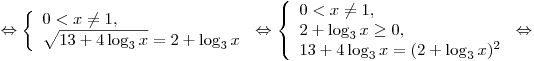
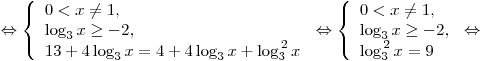
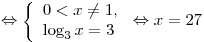 . .
Ответ: 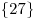 . .
C2. Найдите все значения p, при которых уравнение
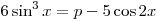 не имеет корней. не имеет корней.
Решение.
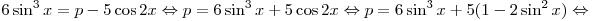
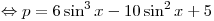 . .
Уравнение не имеет решений при
всех p, не принадлежащих множеству значений функции 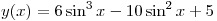 , совпадающему со множеством значений
функции , совпадающему со множеством значений
функции 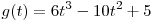 на отрезке на отрезке ![[ -
1;\,\,1] [ -
1;\,\,1]](/inc/pictures/eb34300e7789a73290ce402c8c22bf32.png) . Найдем это множество: . Найдем это множество:
Имеем: 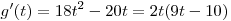 . (см.рис) . (см.рис)
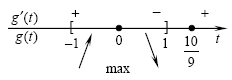
Тогда
а) ![\mathop {\max }\limits_{[ - 1;\,\,1]} g(t) = g_{\max } = g(0)
= 5 \mathop {\max }\limits_{[ - 1;\,\,1]} g(t) = g_{\max } = g(0)
= 5](/inc/pictures/fd74590f3c9864fe05fb622240be89da.png) ; ;
б) 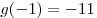 , , 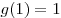 и, так как и, так как
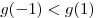 , имеем , имеем ![\mathop {\min }\limits_{[ -
1;\,\,1]} g(t) = g( - 1) = - 11 \mathop {\min }\limits_{[ -
1;\,\,1]} g(t) = g( - 1) = - 11](/inc/pictures/0dd0f24d91dc27c6eda946eb4fcc1e3c.png) . Так как функция . Так как функция 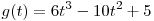 непрерывна на отрезке непрерывна на отрезке ![[ - 1;\,\,1] [ - 1;\,\,1]](/inc/pictures/316658a37e1f318f7c1e7b96cf272c3b.png) ,
ее множество значений – отрезок ,
ее множество значений – отрезок ![[ - 11;\,\,5] [ - 11;\,\,5]](/inc/pictures/6846761c703e64c0b39aff66fadd9845.png) . .
Таким образом, уравнение не имеет
решений для 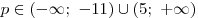 . .
Ответ: 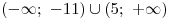 . .
C3. Около правильной шестиугольной призмы описан цилиндр.
Площадь боковой поверхности цилиндра равна 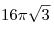 .
Расстояние между осью цилиндра и диагональю боковой грани призмы равно .
Расстояние между осью цилиндра и диагональю боковой грани призмы равно
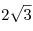 . Найдите объем призмы. . Найдите объем призмы.
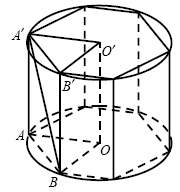 Решение. Введем обозначения, как показано на рисунке. Решение. Введем обозначения, как показано на рисунке.
1. Площадь боковой поверхности цилиндра равна:
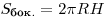 , ,
где R — радиус основания цилиндра, H — его
высота.
Тогда
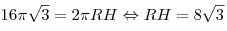 . .
2. Расстояние между двумя скрещивающимися прямыми равно
расстоянию между одной из прямых и параллельной ей плоскостью,
содержащей вторую прямую. Тогда расстояние между осью цилиндра и
диагональю боковой стороны призмы есть расстояние от прямой
 до плоскости до плоскости  , которое равно
высоте треугольника AOB, проведенной из точки O. , которое равно
высоте треугольника AOB, проведенной из точки O.
3. Так как треугольник AOB равносторонний, его высота есть
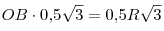 , откуда , откуда
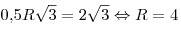 . .
4. Объем призмы равен:
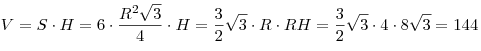 . .
Ответ: 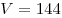 . .
C4. Найдите все значения параметра a, при которых
область определения функции 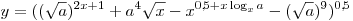 содержит два
или три целых числа. содержит два
или три целых числа.
Решение. По смыслу задачи: 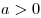 , , 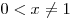 . .
Поскольку степень с дробным положительным показателем определена
только для неотрицательного основания, область определения данной
функции задается неравенством 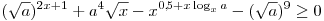 . Решим это
неравенство: . Решим это
неравенство:
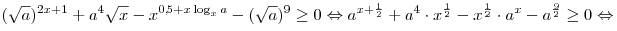
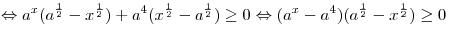 . .
При 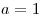 решениями неравенства являются все допустимые
значения x, и область определения данной функции содержит
бесконечное множество целых чисел. решениями неравенства являются все допустимые
значения x, и область определения данной функции содержит
бесконечное множество целых чисел.
Решим последнее неравенство при 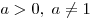 методом
интервалов:. методом
интервалов:.
Имеем:
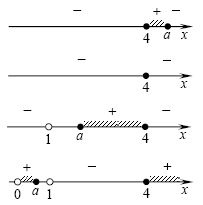
1. При 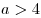 : ООФ – отрезок : ООФ – отрезок ![[4;\,\,a] [4;\,\,a]](/inc/pictures/615e9db1b2420a05dc28c638da4b80f7.png) . .
2. При 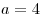 : ООФ – множество : ООФ – множество 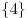 . .
3. При 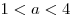 : ООФ – отрезок : ООФ – отрезок
![[a;\,\,4] [a;\,\,4]](/inc/pictures/2b065e2f648cfc30f654b63a80a3ac39.png) . .
4. При 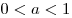 : ООФ – множество : ООФ – множество![(0;\,\,a]
\cup [4;\,\, + \infty ) (0;\,\,a]
\cup [4;\,\, + \infty )](/inc/pictures/1632a272b1e1d04ed8f7f42ed2ec9e1e.png) . .
В первом случае ООФ содержит 2 или
3 целых числа, если 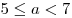 , во втором случае –
ни при каких a, в третьем – при , во втором случае –
ни при каких a, в третьем – при 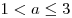 ,
в четвертом – ни при каких a. ,
в четвертом – ни при каких a.
Ответ: ![a \in (1;\,\,3] \cup [5;\,\,7) a \in (1;\,\,3] \cup [5;\,\,7)](/inc/pictures/dd36c38e3036b7be4cbe8609f10d289b.png) . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
