|
Единый государственный экзамен по математике, 2004 год
Часть A
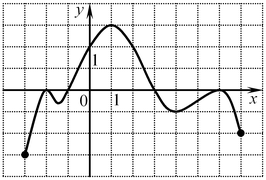 A1. Функция задана графиком. Укажите промежуток, на котором она принимает только положительные значения.
A1. Функция задана графиком. Укажите промежуток, на котором она принимает только положительные значения.
A2. Найдите множество значений функции 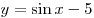 . .
A3. Найдите производную функции 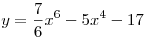 . .
A4. Укажите область определения функции 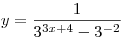 . .
A5. Вычислите: 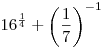 . .
A6. Упростите выражение ![\frac{{\sqrt[5]{{a^{11}}}}}{{\sqrt[5]{a}}} \frac{{\sqrt[5]{{a^{11}}}}}{{\sqrt[5]{a}}}](/inc/pictures/0a4637c1c78be4205290f494c2542218.png) . .
A7. Вычислите: 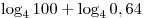 . .
A8. Решите неравенство 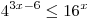 . .
A9. Какому промежутку принадлежит корень уравнения 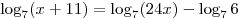 ? ?
A10. Решите неравенство 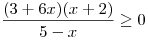 . .
A11. Решите уравнение 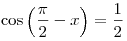 . .
| 1. |
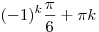 , , 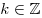 |
2. |
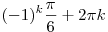 , , 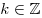 [/tex] [/tex] |
| 3. |
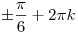 , , 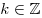 |
4. |
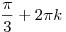 , , 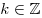 |
A12. К графику функции 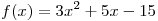 в точке с абсциссой в точке с абсциссой 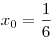 проведена касательная. Найдите тангенс угла наклона касательной к оси проведена касательная. Найдите тангенс угла наклона касательной к оси 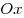 . .
A13. Найдите значение 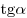 , если , если 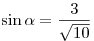 и и 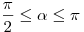 . .
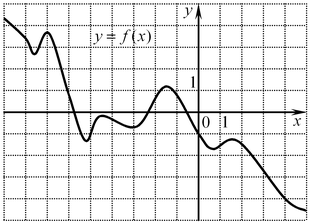 A14. На рисунке изображен график функции
A14. На рисунке изображен график функции 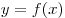 . Какому из следующих промежутков принадлежит корень уравнения . Какому из следующих промежутков принадлежит корень уравнения 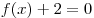 ? ?
Часть B
B1. Вычислите площадь фигуры, ограниченной линиями 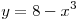 , , 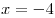 , , 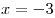 и и 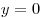 . .
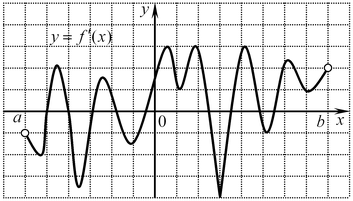 B2. Функция
B2. Функция  определена на промежутке определена на промежутке 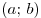 . На рисунке изображен график ее производной.
Укажите число точек минимума функции . На рисунке изображен график ее производной.
Укажите число точек минимума функции  на промежутке на промежутке 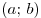 . .
B3. Найдите значение выражения 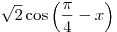 , если , если 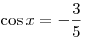 и и 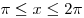 . .
B4. Сколько корней имеет уравнение 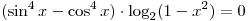 ? ?
B5. Найдите точку максимума функции 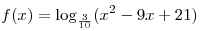 . .
B6. Укажите наименьшее целое число из области определения функции 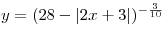 . .
B7. Компьютерная игра состоит в последовательном
прохождении нескольких уровней. За прохождение каждого уровня игрок
получает 10 баллов. Кроме того, начисляются премиальные баллы по
следующей схеме: 4 балла за второй уровень, а за каждый следующий
уровень на 4 балла больше, чем за предыдущий. Сколько уровней надо
пройти, чтобы набрать ровно 570 баллов?
B8. Сечение правильной четырехугольной пирамиды проходит через сторону основания и середину скрещивающегося с ней бокового
ребра. Найдите тангенс угла между плоскостями основания и сечения пирамиды, если высота пирамиды равна 9, а диагональ основания равна 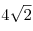 . .
B9. Один из углов прямоугольной трапеции и угол между меньшей диагональю и меньшим основанием раны 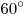 каждый. Найдите большее основание, если средняя линия трапеции равна
каждый. Найдите большее основание, если средняя линия трапеции равна
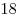 . .
Часть C
C1. Решите систему уравнений 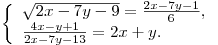
C2. Найдите наименьшее значение периметра прямоугольника со сторонами, параллельными осям координат, и с диагональю 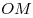 , где , где 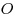 — начало координат, а — начало координат, а  — точка на графике функции — точка на графике функции 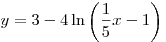 , , 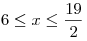 . .
C3. В кубе 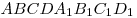 с ребром с ребром
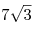 , расположен конус. Вершина конуса находится в
точке , расположен конус. Вершина конуса находится в
точке 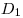 , центр его основания, точка , центр его основания, точка 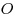 , лежит на
диагонали , лежит на
диагонали 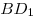 так, что так, что 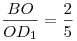 . Окружность основания конуса имеет с каждой гранью, содержащей точку . Окружность основания конуса имеет с каждой гранью, содержащей точку  , ровно по одной общей точке. Определите объем
конуса. , ровно по одной общей точке. Определите объем
конуса.
C4. Найдите все положительные значения параметра  , при каждом из которых множество решений неравенства , при каждом из которых множество решений неравенства 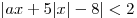 содержится в некотором отрезке длиной содержится в некотором отрезке длиной 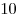 и при этом содержит какой-нибудь отрезок длиной и при этом содержит какой-нибудь отрезок длиной 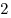 . .
Ответы к заданиям
| A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A8 |
A9 |
A10 |
A11 |
A12 |
A13 |
A14 |
| 1 |
4 |
3 |
4 |
1 |
3 |
3 |
2 |
1 |
4 |
1 |
1 |
2 |
2 |
| B1 |
B2 |
B3 |
B4 |
B5 |
B6 |
B7 |
B8 |
B9 |
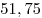 |
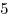 |
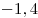 |
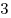 |
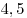 |
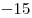 |
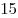 |
 |
 |
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
