|
Единый государственный экзамен по математике, 2007 год
Часть A
A1. Упростите выражение 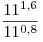 . .
A2. Найдите значение выражения 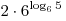 . .
A3. Упростите выражение ![\sqrt[3]{{25n}} \cdot
\sqrt[3]{{5n^2 }} \sqrt[3]{{25n}} \cdot
\sqrt[3]{{5n^2 }}](/inc/pictures/2b5e918fcc2515bf4ba09d76972d1c66.png) . .
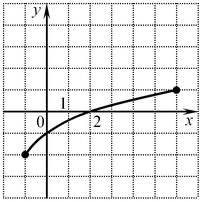 A4. Функция задана графиком. Укажите область определения этой функции.
A4. Функция задана графиком. Укажите область определения этой функции.
A5. Найдите производную функции 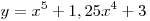 . .
A6. Найдите множество значений функции 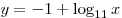 . .
A7. Решите неравенство 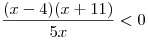 . .
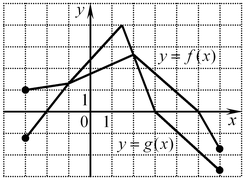 A8. На рисунке изображены графики функций
A8. На рисунке изображены графики функций  и и 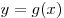 , заданных на промежутке , заданных на промежутке ![[ -3;\,6] [ -3;\,6]](/inc/pictures/6e90538d15d0c4821426c6e06f6a072e.png) . Укажите те значения . Укажите те значения  , для которых выполняется равенство , для которых выполняется равенство 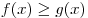 . .
A9. Решите уравнение 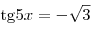 . .
A10. Решите неравенство  . .
Часть B
B1. Решите уравнение 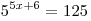 . .
B2. Решите уравнение 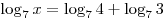 . .
B3. Найдите значение выражения 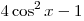 , если , если 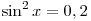 . .
B4. Найдите значение выражения 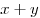 , если , если 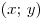 — решение системы — решение системы 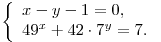
B5. Решите уравнение 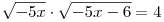 . (Если уравнение имеет более одного корня, то в
бланке ответов запишите произведение его корней.) . (Если уравнение имеет более одного корня, то в
бланке ответов запишите произведение его корней.)
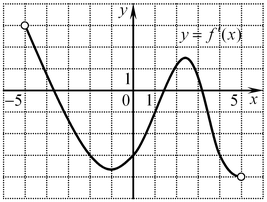 B6. Функция
B6. Функция  определена на промежутке определена на промежутке 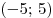 . На рисунке изображен график производной этой функции. К графику функции провели все касательные, параллельные прямой . На рисунке изображен график производной этой функции. К графику функции провели все касательные, параллельные прямой 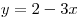 (или совпадающие с ней). Найдите наименьшую из абсцисс точек, в которых проведены эти касательные. (или совпадающие с ней). Найдите наименьшую из абсцисс точек, в которых проведены эти касательные.
B7. Найдите значение выражения
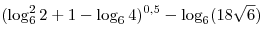 . .
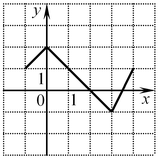 B8. Функция
B8. Функция  определена на всей
числовой прямой и является периодической с периодом 5. На рисунке
изображен график этой функции при определена на всей
числовой прямой и является периодической с периодом 5. На рисунке
изображен график этой функции при 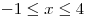 . Найдите
значение выражения . Найдите
значение выражения 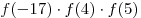 . .
B9. Расстояние между городами  и и  равно равно 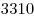 км. Из города км. Из города  в город в город  отправился один поезд, а через час навстречу ему из города отправился один поезд, а через час навстречу ему из города  вышел второй поезд, скорость которого равна на вышел второй поезд, скорость которого равна на 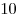 км/ч больше скорости первого. С какой скоростью должен ехать первый поезд, чтобы поезда встретились на станции, расположенной на расстоянии км/ч больше скорости первого. С какой скоростью должен ехать первый поезд, чтобы поезда встретились на станции, расположенной на расстоянии 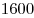 км от города км от города  ? ?
B10. В основании конуса проведена хорда. Через данную хорду и вершину конуса 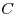 проведена плоскость так, что угол при вершине проведена плоскость так, что угол при вершине 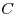 образовавшегося в сечении треугольника равен образовавшегося в сечении треугольника равен
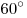 . Найдите расстояние от центра основания конуса . Найдите расстояние от центра основания конуса 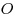 до данной плоскости, если высота конуса равна до данной плоскости, если высота конуса равна 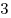 , а образующая равна , а образующая равна 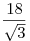 . .
B11. Правильный шестиугольник 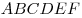 вписан в окружность радиуса вписан в окружность радиуса 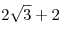 . Найдите радиус окружности, вписанной в треугольник . Найдите радиус окружности, вписанной в треугольник 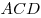 . .
Часть C
C1. Найдите точки минимума функции
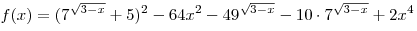 . .
C2. Решите уравнение 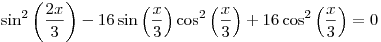 . .
C3. Найдите все значения  , для которых при каждом , для которых при каждом  из промежутка из промежутка ![( - 5;\, - 2] ( - 5;\, - 2]](/inc/pictures/ae92b12cc0c475f19cbe310ba4f6a716.png) значение выражения значение выражения 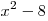 не равно значению выражения не равно значению выражения 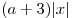 . .
C4. Дан прямоугольный параллелепипед 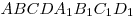 . На его боковых ребрах . На его боковых ребрах 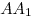 и и 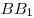 лежат точки лежат точки  и и 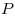 соответственно так, что соответственно так, что
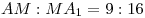 , , 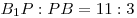 . Во сколько
раз объем данного параллелепипеда больше объема пирамиды с вершиной в
точке . Во сколько
раз объем данного параллелепипеда больше объема пирамиды с вершиной в
точке 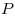 , основанием которой является сечение данного
параллелепипеда плоскостью , основанием которой является сечение данного
параллелепипеда плоскостью 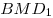 ? ?
C5. Докажите, что система уравнений
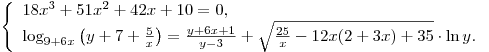
не имеет решений.
Ответы к заданиям
| A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A8 |
A9 |
A10 |
| 4 |
1 |
4 |
2 |
3 |
2 |
2 |
3 |
1 |
3 |
| B1 |
B2 |
B3 |
B4 |
B5 |
B6 |
B7 |
B8 |
B9 |
B10 |
B11 |
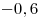 |
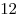 |
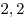 |
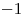 |
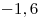 |
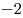 |
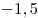 |
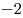 |
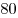 |
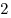 |
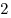 |
| C1 |
C2 |
C3 |
C4 |
C5 |
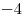 |
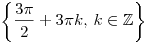 |
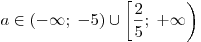 |
В 14 раз |
- |
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
