|
Единый государственный экзамен по математике, 2001 год
Часть A
A1. Найдите значение выражения ![(2\sqrt 5 )^2 - \sqrt[3]{{125}} (2\sqrt 5 )^2 - \sqrt[3]{{125}}](/inc/pictures/3c4ae7ac20c16c6eb9e12fdaadefd35b.png) . .
A2. Упростите выражение 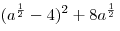 . .
A3. Упростите выражение 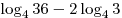 . .
A4. Решите неравенство 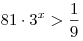 . .
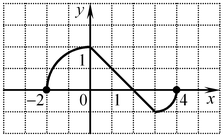 A5. Укажите промежуток убывания функции
A5. Укажите промежуток убывания функции  , заданной графиком. , заданной графиком.
A6. Упростите выражение 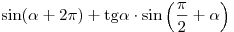 . .
A7. Найдите производную функции 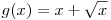 . .
A8. Укажите промежуток, которому принадлежит корень уравнения 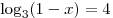 . .
A9. Найдите область определения функции 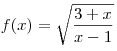 . .
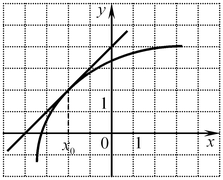 A10. Найдите значение производной функции
A10. Найдите значение производной функции  в точке в точке 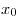 , заданной графиком. , заданной графиком.
A11. Найдите наименьшее значение функции 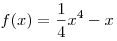 на отрезке на отрезке ![[0;\,2] [0;\,2]](/inc/pictures/fc0441ee3fa76e443cde8129362cf539.png) . .
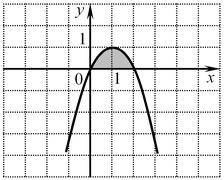 A12. Найдите площадь фигуры, ограниченной линиями
A12. Найдите площадь фигуры, ограниченной линиями 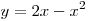 , , 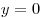 . .
A13. Решите уравнение 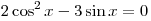 . .
Часть B
B1. Решите уравнение 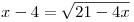 . .
B2. Найдите значение выражения 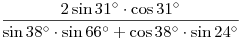 . .
B3. Найдите точку минимума функции 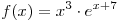 . .
B4. Найдите меньший корень уравнения 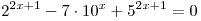 . .
B5. Катер прошел по течению реки расстояние от пункта  до пункта до пункта  за за 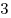 ч., а от ч., а от  до до  — за — за 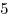 ч. За сколько часов проплывет от ч. За сколько часов проплывет от  до до  плот? плот?
B6. Найдите число целых решений неравенства 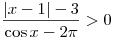 . .
B7. Найдите наименьшее целое значение параметра  , при котором решение системы уравнений , при котором решение системы уравнений 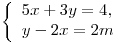 удовлетворяет неравенству удовлетворяет неравенству 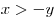 . .
B8. Высота основания правильной треугольной пирамиды равна 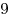 , боковые грани накло¬нены к плоскости основания под углом , боковые грани накло¬нены к плоскости основания под углом 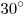 . Найдите площадь боковой поверхности пирамиды. . Найдите площадь боковой поверхности пирамиды.
B9. В конус с образующей 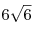 и высотой и высотой 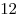 вписан куб. Найдите объем куба. вписан куб. Найдите объем куба.
Часть C
C1. Для каждого допустимого значения параметра  решите неравенство решите неравенство
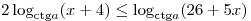 . .
C2. Решите уравнение 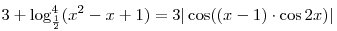
C3. Найдите целые корни уравнения 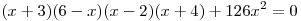 . .
Ответы к заданиям
| A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A8 |
A9 |
A10 |
A11 |
A12 |
A13 |
| 1 |
4 |
2 |
2 |
2 |
3 |
4 |
2 |
4 |
4 |
2 |
2 |
2 |
| B1 |
B2 |
B3 |
B4 |
B5 |
B6 |
B7 |
B8 |
B9 |
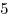 |
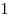 |
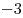 |
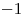 |
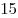 |
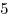 |
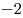 |
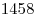 |
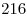 |
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
