|
Преобразования Лоренца
В СТО между координатами и временем в двух ИСО существуют соотношения,
называемые преобразованиями Лоренца. Если СО движутся друг относительно
друга вдоль оси ОХ, то их можно записать в следующем виде.
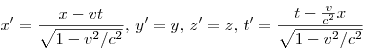
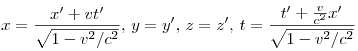
При условии 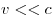 они переходят в преобразования
Галилея. они переходят в преобразования
Галилея.
С учетом преобразований Лоренца принцип относительности можно
сформулировать следующим образом: законы, описывающие любые физические
явления, во всех ИСО должны иметь одинаковый вид. Этот вывод
называется
релятивистской инвариантностью законов физики.
Предыдущий урок Следующий урок
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
