Яблони
Фермер на садовом участке высаживает яблони в форме квадрата, как показано на рисунке. Для защиты яблонь от ветра он сажает по краям участка хвойные деревья. Ниже на рисунке изображены схемы посадки яблонь и хвойных деревьев для нескольких значений  , где , где  — количество рядов высаженных яблонь. Эту последовательность можно продолжить для любого числа — количество рядов высаженных яблонь. Эту последовательность можно продолжить для любого числа  . .
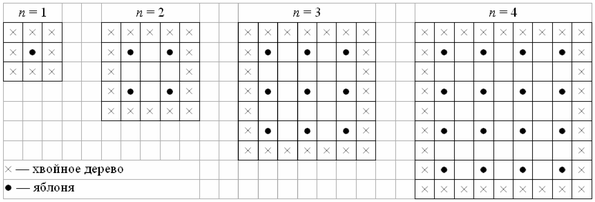
Вопрос 1. Заполните таблицу:
 |
Количество яблонь |
Количество хвойных деревьев |
| 1 |
1 |
8 |
| 2 |
4 |
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
Решение.
1-й способ. Яблони образуют квадрат из  рядов по рядов по  деревьев. Значит, всего яблонь деревьев. Значит, всего яблонь 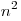 . Вдоль каждой боковой стороны участка высажено . Вдоль каждой боковой стороны участка высажено 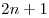 хвойное дерево. При сложении всех четырех боковых сторон каждое из четырех угловых деревьев будет посчитано дважды. Значит хвойных деревьев всего хвойное дерево. При сложении всех четырех боковых сторон каждое из четырех угловых деревьев будет посчитано дважды. Значит хвойных деревьев всего 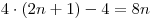 . .
2-й способ. Число хвойных деревьев можно посчитать по-другому. Согласно схеме, между  яблонями садовник оставляет яблонями садовник оставляет 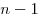 промежуток. Участок внутри хвойных деревьев является квадратом со стороной промежуток. Участок внутри хвойных деревьев является квадратом со стороной 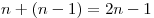 . Длина стороны всего участка вместе с хвойными деревьями составляет . Длина стороны всего участка вместе с хвойными деревьями составляет 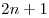 . Тогда число хвойных деревьев равно . Тогда число хвойных деревьев равно  . .
В итоге, таблица выглядит следующим образом:
 |
Количество яблонь |
Количество хвойных деревьев |
| 1 |
1 |
8 |
| 2 |
4 |
16 |
| 3 |
9 |
24 |
| 4 |
16 |
32 |
| 5 |
25 |
40 |
Ответ: см. таблицу.
Вопрос 2. В рассмотренной выше последовательности количество посаженных яблонь и хвойных деревьев подсчитывается следующим образом: количество яблонь 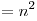 , количество хвойных деревьев , количество хвойных деревьев 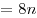 , где , где  — число рядов высаженных яблонь. Для какого значения — число рядов высаженных яблонь. Для какого значения  число яблонь будет равно числу посаженных вокруг них хвойных деревьев? число яблонь будет равно числу посаженных вокруг них хвойных деревьев?
Решение. Решим уравнение:
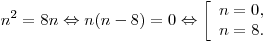
По смыслу задачи число рядов яблонь 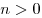 , значит, только при , значит, только при 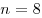 число яблонь совпадет с числом хвойных деревьев. число яблонь совпадет с числом хвойных деревьев.
Ответ: 8.
Вопрос 3. Предположим, что фермер решил постепенно увеличивать число рядов яблонь на своем участке. Что при этом будет увеличиваться быстрее: количество высаживаемых яблонь или количество хвойных деревьев?
Решение. При увеличении на один ряд число хвойных деревьев увеличивается на 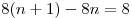 , а число яблонь увеличивается на , а число яблонь увеличивается на 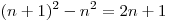 . Видно, что . Видно, что 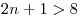 при при 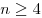 . Начиная с четырех рядов, при последующем увеличении участка число яблонь увеличивается быстрее числа хвойных деревьев. . Начиная с четырех рядов, при последующем увеличении участка число яблонь увеличивается быстрее числа хвойных деревьев.
Ответ: количество высаживаемых яблонь меньше количества хвойных деревьев при увеличении числа рядов яблонь с одного ряда до четырех, при дальнейшем увеличении числа рядов яблонь количество высаживаемых яблонь больше количества хвойных деревьев.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
