Игральные кубики
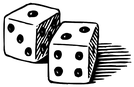
Справа изображены два игральных кубика. Для игральных кубиков выполняется следующее правило: сумма очков, изображенных на двух любых противоположных сторонах кубика, равна семи.
Вопрос 1. Вы можете сделать обычный игральный кубик, вырезая, складывая и склеивая кусочки картона. Это можно сделать разными способами. Ниже изображены четыре развертки куба, на которых нанесены очки. Из каких разверток можно сложить кубик, у которого сумма очков на противоположных сторонах будет равна 7? Обведите слово «Да» или «Нет» в каждой строке следующей таблицы.
| Развертка |
Выполняется ли правило: сумма очков на противоположных сторонах кубика равна 7? |
| I |
Да / Нет |
| II |
Да / Нет |
| III |
Да / Нет |
| IV |
Да / Нет |
Решение. Соединим противоположные грани кубика на его развертке стрелками:
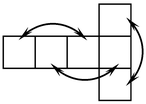
Подсчитаем сумму очков в ячейках, соединенных стрелками. Для первой развертки: 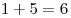 , , 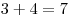 , , 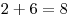 ; для второй: ; для второй: 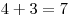 , , 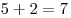 , , 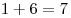 ; для третьей: ; для третьей: 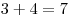 , , 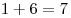 , , 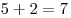 ; для четвертой: ; для четвертой: 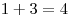 , , 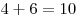 , , 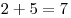 . Правило выполняется только для второй и третьей разверток. . Правило выполняется только для второй и третьей разверток.
Ответ: нет, да, да, нет.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
