Лучший автомобиль
Вопрос 1. Автомобильный журнал использует рейтинговую систему для оценки новых автомобилей и присваивает звание «Автомобиль года» автомобилю, получившему наивысшую общую оценку. Была проведена оценка пяти новых автомобилей, и их рейтинги представлены в таблице.
| Машина |
Обеспечение безопасности
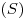 |
Экономия топлива
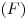 |
Внешний вид
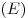 |
Внутренние удобства
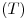 |
| Ca |
3 |
1 |
2 |
3 |
| M2 |
2 |
2 |
2 |
2 |
| Sp |
3 |
1 |
3 |
2 |
| N1 |
1 |
3 |
3 |
3 |
| KK |
3 |
2 |
3 |
2 |
Рейтинги означают следующее:
- 3 очка — превосходно;
- 2 очка — хорошо;
- 1 очко — неплохо.
Вопрос 1. Для подсчета общей оценки машины журнал использует правило, по которому определяется взвешенная сумма всех очков, полученных автомобилем:
Общая оценка 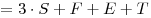 . .
Подсчитайте общую оценку автомобиля «Са».
Решение. Общая оценка автомобиля «Са» равна: 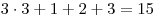 . .
Ответ: 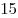 . .
Вопрос 2. Производитель машины «Ca» считает, что правило определения общей оценки несправедливо. Запишите такое правило подсчета общей оценки, чтобы машина «Ca» стала победителем. Ваше правило должно включать все четыре величины, и его надо записать, вставив соответствующие положительные числа в четыре места, обозначенные точками в приведенном ниже выражении.
Общая оценка 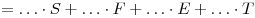 . .
Решение. За обеспечение безопасности и внутренние удобства машина «Ca» получила наивысший балл, поэтому коэффициенты при  и и 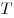 следует брать как можно больше. А за экономию топлива и внешний вид у машины «Ca» низкие оценки, коэффициенты при следует брать как можно больше. А за экономию топлива и внешний вид у машины «Ca» низкие оценки, коэффициенты при 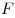 и и 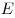 следует брать как можно меньше. Например, правило подсчета может быть таким: следует брать как можно меньше. Например, правило подсчета может быть таким:
Общая оценка 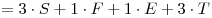 . .
Ответ: например, общая оценка 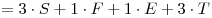 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
