Тестовые оценки
Вопрос 1. Ниже на столбчатой диаграмме представлены результаты выполнения теста по биологии группами учащихся, обозначенными как Группа  и Группа и Группа  . Средняя оценка группы . Средняя оценка группы  равна равна 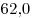 и средняя оценка Группы и средняя оценка Группы  равна равна 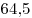 . Считается, что учащийся справился с тестом, если его оценка . Считается, что учащийся справился с тестом, если его оценка 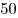 или более баллов. Посмотрев на диаграмму, учительница сделала вывод о том, что Группа или более баллов. Посмотрев на диаграмму, учительница сделала вывод о том, что Группа  выполнила тест лучше, чем Группа выполнила тест лучше, чем Группа  . .
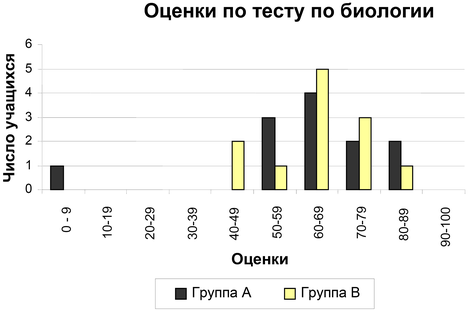
Учащиеся Группы  не согласны с ее мнением. Они стараются убедить учительницу в том, что учащиеся Группы В не обязательно выполнили тест лучше них. Используя диаграмму, приведите один математический довод, которым могли бы воспользоваться учащиеся Группы не согласны с ее мнением. Они стараются убедить учительницу в том, что учащиеся Группы В не обязательно выполнили тест лучше них. Используя диаграмму, приведите один математический довод, которым могли бы воспользоваться учащиеся Группы  . .
Решение. Доводы могут быть следующие. 1) В группе  только один ученик не справился с тестом, а в группе только один ученик не справился с тестом, а в группе  — двое (те, кто набрал менее — двое (те, кто набрал менее 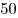 баллов). 2) В то же время число учеников, набравших более баллов). 2) В то же время число учеников, набравших более 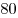 баллов, в группе баллов, в группе  — двое, а в группе — двое, а в группе  — только один. 3) Если не рассматривать самого слабого ученика, набравшего менее — только один. 3) Если не рассматривать самого слабого ученика, набравшего менее 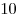 баллов, то средний балл группы баллов, то средний балл группы  будет больше среднего балла группы будет больше среднего балла группы  . .
Ответ: любой из приведенных доводов.
Примечание. Погрешность разницы в баллах достаточно велика для того, чтобы утверждать, что одна группа превзошла другую. Оценим стандартное отклонение средних баллов двух групп:
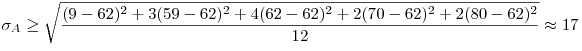 , ,
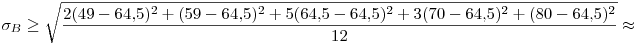
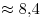 . .
Средний балл группы  равен равен 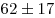 , средний балл группы , средний балл группы  — — 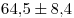 . В пределах погрешности результаты совпадают. . В пределах погрешности результаты совпадают.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
