Теория вероятностей
Вероятность — числовая характеристика степени возможности
появления какого-либо события в тех или иных условиях.
Классическое определение вероятности
Вероятностью события  называется отношение числа
исходов называется отношение числа
исходов  , благоприятствующих его наступлению к числу всех
исходов , благоприятствующих его наступлению к числу всех
исходов  (несовместных, единственно возможных и
равновозможных): (несовместных, единственно возможных и
равновозможных): 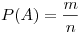 . .
Будем различать достоверные и невозможные события. По определению, их
вероятности соответственно равны 1 и 0.
Геометрическое определение вероятности
Если число исходов некоторого опыта бесконечно, то классическое
определение вероятности не может служить характеристикой степени
возможности наступления того или иного события. В этом случае
пользуются геометрическим подходом к определению вероятности. При этом
вероятность события  есть отношение меры есть отношение меры  (длины, площади, объема) к мере
(длины, площади, объема) к мере 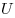 пространства элементарных
событий. пространства элементарных
событий.
Теоремы о вероятностяхсобытий
Произведением событий  и и  называется
событие называется
событие 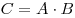 , состоящее в том, что в результате
испытания произошло и событие , состоящее в том, что в результате
испытания произошло и событие  , и событие , и событие  , т.
е. оба события произошли. , т.
е. оба события произошли.
Два события  и и  называются
независимыми, если вероятность появления каждого из них не зависит
от того, появилось другое событие или нет. В противном случае события называются
независимыми, если вероятность появления каждого из них не зависит
от того, появилось другое событие или нет. В противном случае события
 и и  называются зависимыми. называются зависимыми.
Теорема. Вероятность произведения двух независимых событий
 и и  равна произведению этих вероятностей: равна произведению этих вероятностей:
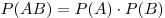 . .
Противоположные события
Два события называются совместными, если появление одного из
них не исключает появление другого в одном и том же испытании.
Два события называются противоположными, если в данном
испытании они несовместны и одно из них обязательно происходит.
Вероятности противоположных событий в сумме дают 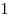 . .
Если событие  может произойти с вероятностью может произойти с вероятностью  и опыт повторяют
и опыт повторяют  раз, то вероятность, что оно наступит
хотя бы один раз, есть: раз, то вероятность, что оно наступит
хотя бы один раз, есть: 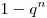 , где , где 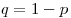 . .
Сложение вероятностей
Суммой событий  и и  называется событие называется событие
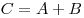 , состоящее в наступлении, по крайней мере, одного
из событий , состоящее в наступлении, по крайней мере, одного
из событий  или или  , т. е. в наступлении
события , т. е. в наступлении
события  , или события , или события  , или обоих этих событий
вместе, если они совместны. , или обоих этих событий
вместе, если они совместны.
Теорема. Вероятность суммы двух несовместных событий
 и и  равна сумме вероятностей этих событий: равна сумме вероятностей этих событий:
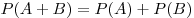 . .
Условная вероятность
Пусть  и и  — зависимые события.
Условной вероятностью — зависимые события.
Условной вероятностью 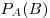 события события  называется вероятность события
называется вероятность события  , найденная в предположении,
что событие , найденная в предположении,
что событие  уже наступило. уже наступило.
Теорема. Вероятность произведения двух зависимых событий
 и и  равна произведению вероятности одного из
них на условную вероятность другого, найденного в предположении, что
первое событие уже наступило: равна произведению вероятности одного из
них на условную вероятность другого, найденного в предположении, что
первое событие уже наступило: 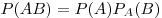 . .
Теорема. Вероятность суммы двух совместных событий  и
и  равна сумме вероятностей этих событий минус вероятность
их произведения: равна сумме вероятностей этих событий минус вероятность
их произведения: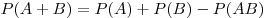 . .
Формула Бернулли
Для многократно повторяемых опытов справедлива формула Бернулли:
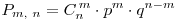 , где , где
 — число удачных исходов среди проводимых — число удачных исходов среди проводимых
 опытов, опытов,  — вероятность наступления
благоприятного исхода в единичном опыте, — вероятность наступления
благоприятного исхода в единичном опыте, 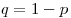 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
