Функция арккотангенс
Арккотангенсом числа  называется такой угол называется такой угол
 , для которого , для которого 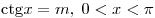 . .

График функции 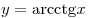
Функция 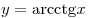 непрерывна и ограничена. непрерывна и ограничена.
Функция 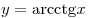 является строго убывающей. является строго убывающей.
Свойства функции арккотангенс:
Таким образом, график функции центрально-симметричен относительно
точки 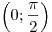 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
