Функция арктангенс
Арктангенсом числа  называется такое число называется такое число
 , для которого , для которого 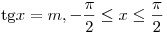 . .
 График функции
График функции 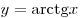 . .
Функция 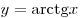 непрерывна и
ограничена. непрерывна и
ограничена.
Функция 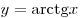 является строго
возрастающей. является строго
возрастающей.
Свойства функции арктангенс:
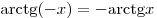 (функция нечётная). (функция нечётная).
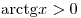 при при 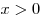 . .
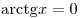 при при  . .
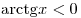 при при 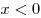 . .
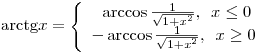
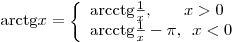
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
