Функция арккосинус
Арккосинусом числа  называется такое число называется такое число
 , для которого , для которого 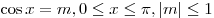
 График функции
График функции 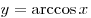 . .
Функция 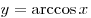 непрерывна и ограничена. непрерывна и ограничена.
Функция 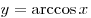 является строго убывающей. является строго убывающей.
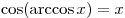 при при 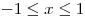 . .
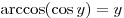 при при 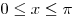 . .
![D(\arccos x) = [ - 1;1] D(\arccos x) = [ - 1;1]](/inc/pictures/33d5c863cef9ae6c2dac2007bfe77c19.png) (область определения), (область определения),
![E(\arccos x) = [0;\pi ] E(\arccos x) = [0;\pi ]](/inc/pictures/7f39625640e28859581dcb4b34a8304c.png) (область значений). (область значений).
Свойства функции арккосинус:
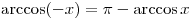 (график функции
центрально-симметричен относительно точки (график функции
центрально-симметричен относительно точки 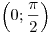 .) .)
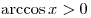 при при 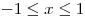 . .
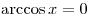 при при  . .
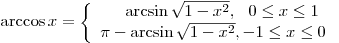
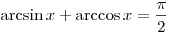
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
