Функция арксинус
Арксинусом
числа  называется такое число называется такое число  , для которого , для которого
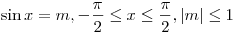 . .
 График функции
График функции 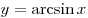 . .
Функция 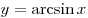 непрерывна и ограничена. непрерывна и ограничена.
Функция 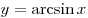 является строго возрастающей. является строго возрастающей.
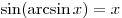 при при 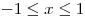
 при при 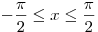
![D(\arcsin x) = [ - 1;1] D(\arcsin x) = [ - 1;1]](/inc/pictures/37cb054b360f09efd2a8dc8abecd8627.png) (область определения), (область определения),
![E(\arcsin x) = \left[ { - \frac{\pi }{2};\frac{\pi }{2}}
\right] E(\arcsin x) = \left[ { - \frac{\pi }{2};\frac{\pi }{2}}
\right]](/inc/pictures/7234b6b591668ee1ac6c66bd3ec905c6.png) (область значений). (область значений).
Свойства функции арксинус:
 (функция является нечётной). (функция является нечётной).
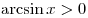 при при 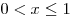 . .
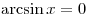 при при  . .
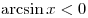 при при 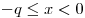 . .
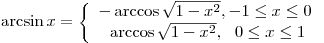
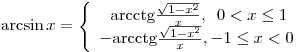
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
