Формулы приведения
Все формулы приведения получаются из соответствующих формул сложения.
Применение формул приведения можно свести к использованию мнемонического правила:
- Определяется название приведенной функции по следующему правилу: если аргумент приводимой функции имеет вид
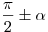 или или 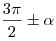 , то функция меняется на сходственную, если аргумент приводимой функции имеет вид , то функция меняется на сходственную, если аргумент приводимой функции имеет вид 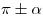 , то функция названия не меняет. , то функция названия не меняет.
- Определяется координатная четверть, в которой лежит аргумент приводимой функции, в предположении, что
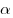 — острый угол, и определяется знак приводимой функции в этой четверти. — острый угол, и определяется знак приводимой функции в этой четверти.
Формулы приведения
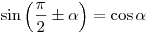 ; ;
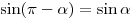 ; ;
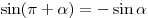 ; ;
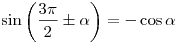 ; ;
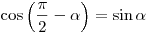 ; ;
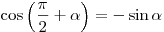 ; ;
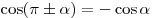 ; ;
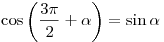 ; ;
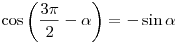 ; ;
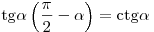 ; ;
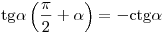 ; ;
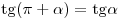 ; ;
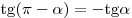 ; ;
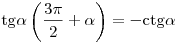 ; ;
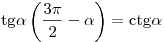 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
