Интеграл и его вычисление
Определение. Множество первообразных данной функции 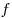 называют неопределённым интегралом (общим интегралом)
называют неопределённым интегралом (общим интегралом)
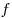 . .
Определение. Определенным интегралом функции f(x) на отрезке
![[a,b] [a,b]](/inc/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) называется число, равное площади части плоскости, ограниченной
прямыми называется число, равное площади части плоскости, ограниченной
прямыми 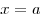 , , 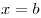 , кривой , кривой 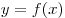 и осью и осью 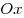 . .
Формула вычисления определенных интегралов
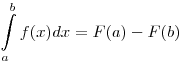 (Формула
Ньютона-Лейбница). (Формула
Ньютона-Лейбница).
Площадь криволинейной трапеции – части плоскости,
ограниченной прямыми 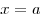 , ,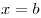 , где , где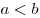 , кривой , кривой  и осью Ox, находится по
формуле и осью Ox, находится по
формуле
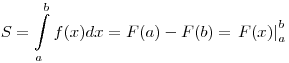
Если фигура ограничена сверху кривой 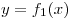 , а снизу
— кривой , а снизу
— кривой 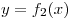 для всех для всех ![x \in
[a;b] x \in
[a;b]](/inc/pictures/b106c77d38ce137b8d01a240449d83b4.png) , то ее площадь вычисляется по формуле: , то ее площадь вычисляется по формуле:
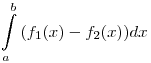
Объем тела вращения, образованного вращением вокруг оси Ox
криволинейной трапеции 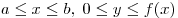 ,
равен ,
равен
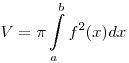
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
