Первообразная
Определение. Функция 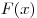 называется первообразной
для называется первообразной
для 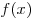 на промежутке, если на промежутке, если 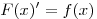 на этом
промежутке. Все первообразные функции на этом
промежутке. Все первообразные функции 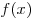 запишутся в
виде запишутся в
виде 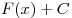 , где , где 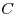 — все возможные постоянные. — все возможные постоянные.
Правила вычисления первообразных
Если 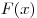 — первообразная для — первообразная для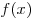 , а , а 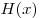 — первообразная для — первообразная для 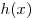 , то: , то:
- F(x) + H(x) — первообразная для f(x) + h(x)
- kF(x) — первообразная для kf(x)
- F(kx + b)/k— первообразная для
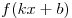
Основные первообразные (добавление констант в правой части опущено)
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
