Промежутки выпуклости функции. Точки перегиба
Определение 1. Функция 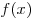 называется выпуклой
вверх (вниз) в точке называется выпуклой
вверх (вниз) в точке  , если ее график в некоторой окрестности
точки , если ее график в некоторой окрестности
точки  лежит ниже (выше) касательной, проведенной к графику
функции лежит ниже (выше) касательной, проведенной к графику
функции 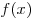 в точке с абсциссой, равной в точке с абсциссой, равной  . .
Определение 2. Если в любой точке  множества множества 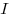 ,
функция выпукла вверх (вниз), то такую функцию называют выпуклой вверх
(вниз) на промежутке ,
функция выпукла вверх (вниз), то такую функцию называют выпуклой вверх
(вниз) на промежутке 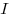 . .
Определение 3. Второй производной функции 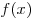 называется функция, являющаяся производной от производной функции
называется функция, являющаяся производной от производной функции
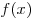 . .
Теорема. Если функция  имеет положительную
(отрицательную) вторую производную в каждой точке промежутка имеет положительную
(отрицательную) вторую производную в каждой точке промежутка
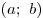 , то , то  выпукла вниз (вверх) на
этом промежутке. выпукла вниз (вверх) на
этом промежутке.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
