Экстремумы функции
Определение 1. Точка 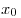 называется точкой
максимума [точкой минимума] функции называется точкой
максимума [точкой минимума] функции  ,
если существует такая ,
если существует такая 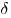 - окрестность - окрестность 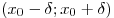 точки точки 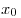 , что для всех
значений , что для всех
значений 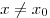 из этой окрестности выполняется
неравенство из этой окрестности выполняется
неравенство 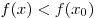 ![[f(x) > f(x_0 )] [f(x) > f(x_0 )]](/inc/pictures/d92c8ab6ef9f110ad6fe2df0fc32ab5c.png) . .
Определение 2. Значение функции в точке максимума (точке
минимума) называется максимумом (минимумом) функции
 . .
Определение 3. Точки минимума и точки максимума называются
точками экстремума функции  , а значения
функции в этих точках — экстремумами функции , а значения
функции в этих точках — экстремумами функции 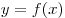 . .
Теорема 1. Если функция  непрерывна в точке непрерывна в точке
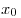 , а , а 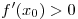 на промежутке на промежутке
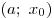 и и 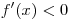 на промежутке на промежутке 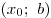 , то , то 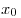 является точкой максимума функции является точкой максимума функции
 . .
Теорема 2. Если функция  непрерывна в точке непрерывна в точке
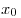 , а , а 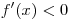 на промежутке на промежутке 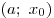 и и 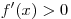 на промежутке на промежутке 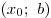 ,
то ,
то 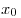 — точка минимума функции — точка минимума функции  . .
Теорема 3 (Ферма). Пусть функция 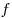 определена в
некоторой окрестности точки определена в
некоторой окрестности точки 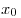 и дифференцируема в этой
точке. Если и дифференцируема в этой
точке. Если 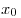 — точка экстремума функции — точка экстремума функции
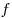 , то , то 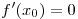 . .
Теорема 4. Пусть функция 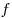 дифференцируема в
некоторой окрестности точки дифференцируема в
некоторой окрестности точки 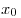 , кроме, быть может, самой
точки , кроме, быть может, самой
точки 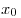 , и непрерывна в точке , и непрерывна в точке 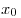 . Тогда,
если . Тогда,
если 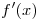 меняет знак с « меняет знак с « » на
« » на
«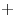 » (с « » (с «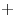 » на
« » на
« ») при переходе через точку ») при переходе через точку 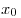 ,
то ,
то 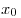 — точка минимума (точка максимума)
функции — точка минимума (точка максимума)
функции 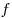 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
