Промежутки монотонности функции
Определение. Функция  называется
возрастающей на множестве называется
возрастающей на множестве 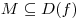 , если для
любых значений аргумента , если для
любых значений аргумента 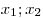 из из  выполняется условие
выполняется условие 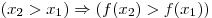 . .
Теорема 1. Если функция  имеет положительную
(отрицательную) производную в каждой точке промежутка имеет положительную
(отрицательную) производную в каждой точке промежутка
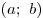 , то , то  возрастает (убывает) на
этом промежутке. возрастает (убывает) на
этом промежутке.
Теорема 2. Если функция непрерывна на промежутке
![[a;\,\,b] [a;\,\,b]](/inc/pictures/bdae212ad71592a3e4f39c68268d7388.png) и возрастает (убывает) на промежутке и возрастает (убывает) на промежутке
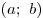 , то она возрастает (убывает) и на промежутке , то она возрастает (убывает) и на промежутке
![[a;\,\,b] [a;\,\,b]](/inc/pictures/bdae212ad71592a3e4f39c68268d7388.png) . .
Промежутки, на которых функция  возрастает
(убывает) называются промежутками монотонности функции возрастает
(убывает) называются промежутками монотонности функции 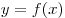 . .
Замечание. Функция возрастающая (убывающая) на всей
области определения называется возрастающей (убывающей)
функцией.
Замечание. Функция, возрастающая (убывающая) на каждом из
нескольких промежутках не обязательно убывает на их объединении.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
