Производная и ее свойства
Определение: Пусть функция 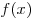 определена в точке определена в точке
 и в некоторой ее окрестности. Дадим аргументу и в некоторой ее окрестности. Дадим аргументу  приращение
приращение 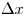 , такое, чтобы не выйти из указанной
окрестности. Найдем соответствующее приращение функции , такое, чтобы не выйти из указанной
окрестности. Найдем соответствующее приращение функции 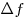 и
составим отношение. Если существует предел этого отношения при и
составим отношение. Если существует предел этого отношения при
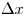 стремящемся к нулю, то указанный предел называют
производной функции стремящемся к нулю, то указанный предел называют
производной функции 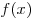 в точке в точке  и обозначают и обозначают 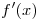 . Иначе говоря: . Иначе говоря:
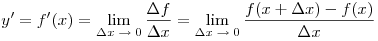 ( (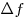 — приращение функции, — приращение функции, 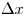 —
приращение аргумента). —
приращение аргумента).
Если в каждой точке 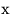 из множества из множества 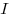 у функции у функции
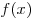 существует производная, то такая функция называется
дифференцируемой на множестве существует производная, то такая функция называется
дифференцируемой на множестве 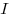 . .
Геометрический смысл производной: 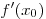 —
угловой коэффициент касательной к графику функции —
угловой коэффициент касательной к графику функции  в
точке в
точке 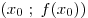 уравнение касательной в этой
точке уравнение касательной в этой
точке 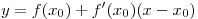 . .
Правила дифференцирования
Пусть функции 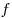 и и 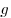 определены и дифференцируемы
на некотором множестве определены и дифференцируемы
на некотором множестве 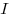 , , 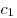 и и 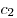 — любые действительные
числа. Тогда на множестве — любые действительные
числа. Тогда на множестве 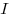 справедливы соотношения: справедливы соотношения:
Основные формулы дифференцирования.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
