Монотонность функции
Определение 1: Функции 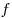 называется возрастающей
[убывающей] на множестве называется возрастающей
[убывающей] на множестве 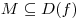 ,
если для любых значений аргумента ,
если для любых значений аргумента 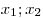 из из  выполняется условие
выполняется условие 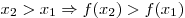 ![[x_2 > x_1 \Rightarrow f(x_2 ) < f(x_1 )] [x_2 > x_1 \Rightarrow f(x_2 ) < f(x_1 )]](/inc/pictures/b5f13aa6c66060934e796b7e8914f840.png) . .
Определение 2: Промежутки области определения, на которых
функция возрастает или убывает, называются промежутками
монотонности функции.
Определение 3: Функция 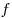 называется возрастающей
[убывающей], если для любых значений аргумента называется возрастающей
[убывающей], если для любых значений аргумента 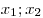 из из 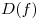 выполняется условие выполняется условие 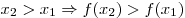 ![[x_2 > x_1 \Rightarrow f(x_2
) < f(x_1 )] [x_2 > x_1 \Rightarrow f(x_2
) < f(x_1 )]](/inc/pictures/5e6804784b5a0d6b5a05e845f2fea87f.png) . .
Определение 4: Возрастающие и убывающие функции называются
монотонными.
Теорема 1. Если функция 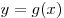 возрастает на
множестве возрастает на
множестве  , а функция , а функция  убывает на
множестве убывает на
множестве  , то уравнение , то уравнение 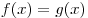 имеет на имеет на
 не более одного корня. не более одного корня.
Теорема 2. Если функция 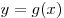 монотонна на
множестве монотонна на
множестве  , а функция , а функция  постоянна на
множестве постоянна на
множестве  , то уравнение , то уравнение 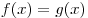 имеет на имеет на
 не более одного корня. не более одного корня.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
