Периодические функции
Функция  называется периодической, если
существует такое число называется периодической, если
существует такое число 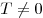 , что выполнены следующие два
условия: , что выполнены следующие два
условия:
если 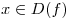 , то , то 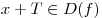 и и 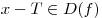 ; ;
для любого 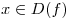 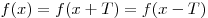 . .
Число 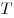 при этом называется периодом функции при этом называется периодом функции 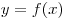 . .
Если числа 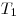 и и 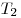 являются периодами
функции являются периодами
функции 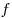 , то и их сумма , то и их сумма 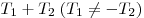 и разность и разность 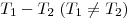 также
являются периодами функции f. также
являются периодами функции f.
Следствие. Если 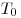 — период функции — период функции
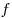 , то число , то число 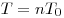 , где , где 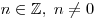 , — также период этой функции. , — также период этой функции.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
