Четные и нечетные функции
Функция  называется четной, если выполнены
следующие два условия: называется четной, если выполнены
следующие два условия:
если 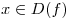 , то , то 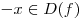 ; ;
для любого 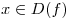 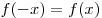 . .
Функция  называется нечетной, если выполнены
следующие два условия: называется нечетной, если выполнены
следующие два условия:
если 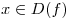 , то , то 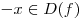 ; ;
для любого 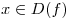 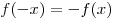 . .
Теорема. Любая функция 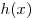 с симметричной
относительно нуля областью определения представима в виде суммы четной
и нечетной функции: с симметричной
относительно нуля областью определения представима в виде суммы четной
и нечетной функции: 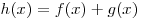 , где , где 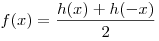 — четная функция, — четная функция, 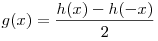 — нечетная функция. — нечетная функция.
Свойство. Функция является четной тогда и только тогда, когда
ее график симметричен относительно оси 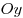 . .
Свойство. Функция является нечетной тогда и только тогда, когда
ее график симметричен относительно точки 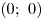
Свойство. Если нечетная функция определена при 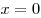 , то , то 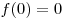 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
