Тригонометрия. Определения
Пусть на плоскости задана прямоугольная система координат с началом в точке 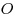 и с осями и с осями 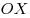 и и 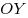 . Возьмем в этой системе координат окружность с центром в точке . Возьмем в этой системе координат окружность с центром в точке 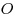 и радиусом, равным единице. Пусть отрезок и радиусом, равным единице. Пусть отрезок 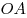 поворачивается от оси поворачивается от оси 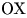 на произвольный угол на произвольный угол 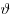 вокруг центра вокруг центра 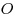 . .
Синусом угла 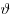 называется ордината точки называется ордината точки  . .
Косинусом угла 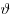 называется абсцисса точки называется абсцисса точки  . .
Тангенсом угла 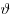 называется отношение ординаты точки называется отношение ординаты точки  к абсциссе точки к абсциссе точки  . Иначе говоря, верна формула: . Иначе говоря, верна формула:
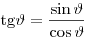 . .
Котангенсом угла 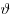 называется отношение абсциссы точки называется отношение абсциссы точки  к ординате точки к ординате точки  . Иначе говоря, верна формула: . Иначе говоря, верна формула:
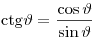 . .
Котангенс равен обратному значению тангенса:
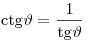 . .
Секансом угла 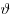 называется величина, обратная косинусу: называется величина, обратная косинусу:
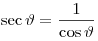 . .
Косекансом угла 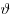 называется величина, обратная синусу: называется величина, обратная синусу:
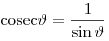 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
