Геометрическая прогрессия
Геометрической прогрессией называется числовая последовательность, каждый член которой отличен от нуля и, начиная со второго, равен предыдущему члену, умноженному на постоянное для данной последовательности число, не равное нулю.
Это постоянное число называется знаменателем геометрической прогрессии и обозначается обычно буквой 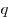 . Геометрическая прогрессия называется возрастающей, если . Геометрическая прогрессия называется возрастающей, если 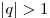 и убывающей, если и убывающей, если 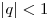 . .
Таким образом, геометрическая прогрессия задается рекуррентным соотношением 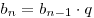 и первым членом и первым членом 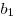 . .
Формула n-го члена геометрической прогрессии
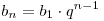 . .
Характеристическое свойство геометрической прогрессии
Числовая последовательность 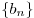 является геометрической прогрессией тогда и только тогда, когда любой член этой последовательности, начиная со второго, удовлетворяет равенству является геометрической прогрессией тогда и только тогда, когда любой член этой последовательности, начиная со второго, удовлетворяет равенству
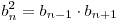 , , 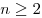 . .
Замечание. Для последовательности с положительными членами характеристическое свойство может быть записано в виде:
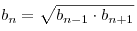 , , 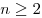 . .
То есть любой член последовательности, начиная со второго, равен среднему геометрическому соседних с ним членов.
Сумма  первых членов геометрической прогрессии обычно обозначается первых членов геометрической прогрессии обычно обозначается 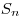 и при и при 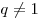 вычисляется по формуле: вычисляется по формуле:
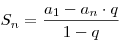 . .
При решении задач, связанных с геометрической прогрессией, могут оказаться полезными также следующие формулы:
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
