Арифметическая прогрессия
Арифметической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с постоянным для данной последовательности числом.
Это постоянное число называется разностью арифметической прогрессии и обозначается обычно буквой 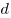 . Арифметическая прогрессия называется возрастающей, если . Арифметическая прогрессия называется возрастающей, если 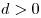 , и убывающей, если , и убывающей, если 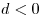 . .
Таким образом, арифметическая прогрессия задается рекуррентным соотношением 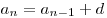 и первым членом и первым членом 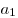 . .
Формула n-го члена арифметической прогрессии
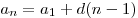 . .
Характеристическое свойство арифметической прогрессии
Числовая последовательность 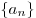 является арифметической прогрессией тогда и только тогда, когда любой член этой последовательности, начиная со второго, есть среднее арифметическое соседних с ним членов: является арифметической прогрессией тогда и только тогда, когда любой член этой последовательности, начиная со второго, есть среднее арифметическое соседних с ним членов:
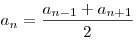 , , 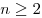 . .
Сумма  первых членов арифметической прогрессии обычно обозначается первых членов арифметической прогрессии обычно обозначается 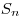 и вычисляется по формуле: и вычисляется по формуле:
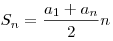 . .
При решении задач, связанных с арифметической прогрессией, могут оказаться полезными также следующие формулы:
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
