Взаимное расположение сферы и плоскости
Если расстояние от центра сферы до плоскости больше радиуса этой
сферы, то сфера и плоскость не имеют общих точек.
Если расстояние от центра сферы до плоскости меньше радиуса этой
сферы, то сечение сферы плоскостью есть окружность.
В этом случае плоскость называется секущей по отношению к
сфере.
Сечение шара плоскостью есть круг. Радиус сечения 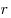 выражается через радиус шара
выражается через радиус шара 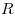 и расстояние и расстояние 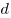 от
центра шара до плоскости сечения следующим образом от
центра шара до плоскости сечения следующим образом
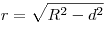 . .
- Если секущая плоскость проходит через центр шара, то
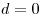 и радиус сечения равен радиусу шара. Такой круг называется большим
кругом шара.
и радиус сечения равен радиусу шара. Такой круг называется большим
кругом шара.
- Если расстояние от центра сферы до плоскости равно радиусу этой сферы,
то сфера и плоскость имеют ровно одну общую точку.
- В этом случае плоскость называется касательной к сфере,
а их общая точка называется точкой касания сферы и плоскости
Объем многогранника, описанного вокруг сферы радиусом 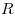 , справедливо равенство:
Где , справедливо равенство:
Где  — полная поверхность многогранника.
Для выпуклого многогранника, все вершины которого расположены в двух параллельных плоскостях объем можно посчитать по формуле:
Где — полная поверхность многогранника.
Для выпуклого многогранника, все вершины которого расположены в двух параллельных плоскостях объем можно посчитать по формуле:
Где 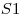 — площадь грани, расположенной в одной плоскости, — площадь грани, расположенной в одной плоскости, 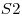 — площадь грани, расположенной в другой плоскости, — площадь грани, расположенной в другой плоскости,  — площадь сечения многогранника плоскостью, равноудаленной от двух данных, — площадь сечения многогранника плоскостью, равноудаленной от двух данных, 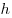 — расстояние между данными плоскостями. — расстояние между данными плоскостями.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
